À fond les formes
De l'utilisation du nombre pi dans les tracés de pistes d'athlétisme
De la géométrie élémentaire pour expliquer comment les miroirs paraboliques concentrent l'énergie solaire
Avec une corde de longueur fixée, délimitez une figure polygonale d'aire maximale (feat. le théorème de Pick)
La légende de Didon et les problèmes isopérimétriques
Systèmes dynamiques
Saurez-vous percer le mystère de l'ordre des étoiles ?
Possible ou impossible ?
Est-il possible de passer à travers une feuille format A5 sans la déchirer ?
Parviendrez-vous à les rendre tous identiques ?
Votre mission : faire sortir tous les sorciers de prison. Mais est-ce vraiment possible ?
Tentez de remettre de l'ordre dans les décimales !
Nombres
Une page regroupant divers documents, activités et tours de magie autour de la suite de Fibonacci et du fascinant nombre d'or.
Une page regroupant divers documents et activités autour du fameux nombre pi.
Un tour de magie où l'on retrouve un nombre mystère à l'aide de l'écriture en base 2 des nombres entiers.
Comprendre les mathématiques cachées derrière ce tour de magie.
Des maths dans la vie de tous les jours
En complément de notre
poster «Les maths ça sert à rien (sauf à...)», nous vous proposons quelques pistes pour aller plus loin et découvrir comment les mathématiques interviennent dans des domaines variés
Expérimentez la transformée en cosinus discrète, au centre de la compression JPEG de vos photos
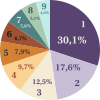
Parmi les nombres rencontrés dans notre vie quotidienne, la loi de Benford affirme que ceux qui commencent par un 1 sont beaucoup plus fréquents que ceux commençant par un 9. Mais est-ce vraiment le cas ?
Fractales
Obtenez un magnifique arbre fractal à partir d'une figure illustrant le fameux théorème de Pythagore : un triangle rectangle et les trois carrés construits sur ses côtés.
Des figures fractales classiques comme le triangle de Sierpinski ou la courbe de Koch sont obtenues comme attracteur d'un
système de fonctions itérées (en anglais : Iterated Function System, ou IFS).
On peut aussi définir soi-même le système et créer des fractales inédites.
Construisez un objet fractal tridimensionnel en origami.
Pliages et découpages
Quelques activités autour des mathématiques et de l'origami.
Très simple à construire, le ruban de Möbius
a des propriétés topologiques vraiment surprenantes !
Pavages
Des activités
autour des fameux pavages apériodiques de Penrose, avec fléchettes et cerfs-volants !
Posters de mathématiques
Une collection de posters sur différents thèmes mathématiques : fractales, origami, courbes, bulles de savons...
L'ancienne version de notre site reste encore accessible.
