À l'occasion de la Fête de la Science, nous avons testé une théorie appelée loi de Benford, selon laquelle les nombres que l'on rencontre dans la vie quotidienne commenceraient beaucoup plus souvent par le chiffre 1 que par le chiffre 9 !
Plus précisément, cette loi de Benford s'intéresse à ce que l'on appelle le premier chiffre significatif de chaque nombre, c'est-à-dire le chiffre le plus à gauche qui n'est pas un zéro dans son écriture en base 10. Par exemple, le premier chiffre significatif de 2018 est 2, celui de 3,14159 est 3, celui de -0,05 est 5. Par définition il n'est jamais zéro donc ce premier chiffre significatif est toujours l'un des chiffres 1, 2, 3, 4, 5, 6, 7, 8 ou 9.
La loi de Benford stipule que les fréquences d'apparition de chacun de ces chiffres au début des nombres que nous rencontrons ne sont pas uniformes : comme indiqué sur le diagramme ci-dessous, presque un tiers des nombres commenceraient par un 1, et les proportions décroissent jusqu'à moins d'un sur vingt pour le chiffre 9 !
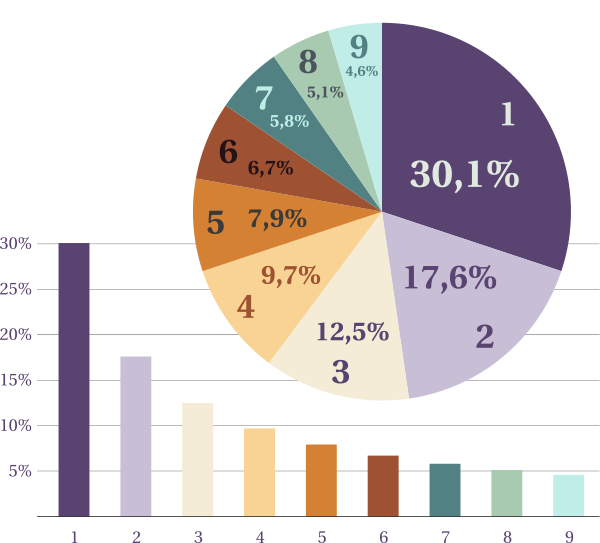
Proportion des nombres commençant par chaque chiffre selon la loi de Benford
Pour ceux qui connaissent la fonction logarithme, ces fréquences théoriques sont même données par une formule mathématique précise : pour $i=1,2,...,9$, la proportion des nombres commençant par le chiffre $i$ est donnée par $$ \log_{10} \frac{i+1}{i}.$$
Nous avons voulu vérifier si effectivement les nombres rencontrés dans la vie de tous les jours étaient en accord avec la loi de Benford. Pour cela, nous avons collecté un grand nombre de documents sur des thèmes variés (journaux quotidiens, de sports, revues de cuisine, de sciences, sur l'automobile, catalogues, prospectus etc.). En effet, Benford lui-même affirmait que cette loi se vérifie d'autant mieux que les données utilisées sont d'origines variées.

Une fois ces documents disposés sur une table de notre stand à la Fête de la Science, nous avons demandé aux visiteurs de participer à notre expérience. Pour cela, chaque volontaire devait choisir l'un des documents sur la table, l'ouvrir à une page au hasard, commencer à lire et relever sur une feuille les dix premiers nombres rencontrés.

Après avoir entouré sur chaque nombre le premier chiffre significatif, le participant enregistrait ensuite ses observations en plaçant un pion dans la colonne correspondante pour chaque chiffre relevé.
La photographie ci-dessous montre les résultats obtenus après une journée d'expérience et plusieurs centaines de nombres relevés. Assez conformes aux prévisions de la loi de Benford, non ?

Pour en savoir plus sur la loi de Benford, en particulier pour en découvrir une utilisation surprenante, nous vous invitons à lire l'article Quel est le début de ce nombre ? sur le site Images des Mathématiques. Vous pourez également télécharger notre poster sur la loi de Benford sur cette page.