Marche aléatoire
Une marche aléatoire est un déplacement où chaque nouveau pas est choisi en faisant intervenir le hasard.

Le héros de bande dessinée Rahan suit une sorte de marche aléatoire : à la fin de chaque épisode il choisit la direction indiquée par son coutelas après l'avoir fait tourner sur une pierre.
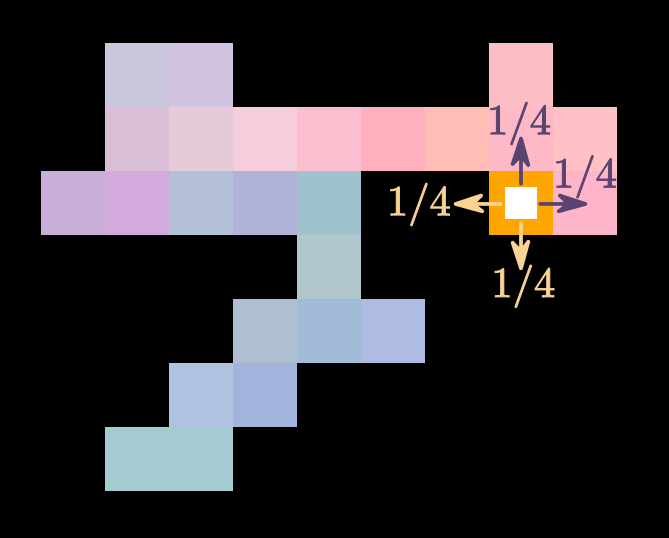
Au début de l'animation, on observe une marche aléatoire simple dans le plan. Dans ce cas la règle est la suivante : à chaque étape, on tire au hasard l'une des quatre directions nord, sud, est, ouest (chacune avec probabilité 1/4), et on avance d'un pas dans cette direction. La fenêtre montre la trajectoire de la marche depuis le début. Les couleurs de la trace laissée par la marche évoluent également au hasard, pour mieux visualiser lorsque la marche repasse par des sites déjà visités.
Changement d'échelle
Lorsque la marche arrive très près du bord de la fenêtre, ou lorsqu'on le demande en cliquant sur le bouton correspondant, on effectue un changement d'échelle. Dans cette opération, toutes les distances sont divisées par 2 : chaque pas de la marche sera ainsi deux fois plus petit qu'auparavant. Le changement d'échelle affecte également le temps entre deux pas de la marche, qui est lui divisé par 4 (dans les limites des possibilités de l'ordinateur !).
Mouvement brownien vs. marche aléatoire
Après avoir effectué un certain nombre de changements d'échelle, l'allure du déplacement a changé et se rapproche de plus en plus de ce que l'on appelle le mouvement brownien plan.

Ce processus limite est lui aussi un déplacement au hasard dans le plan, mais il se distingue de la marche aléatoire en plusieurs aspects.
- La marche aléatoire procède par sauts, et se déplace sur les points du plan à coordonnées entières, tandis que la trajectoire du mouvement brownien est continue et peut atteindre n'importe quel point du plan.
- Dans le cas de la marche aléatoire, les directions Nord/Sud et Est/Ouest sont privilégiées (comme si le coutelas de Rahan ne pouvait prendre que 4 positions possibles), alors que le mouvement brownien est isotrope : il avance de la même façon dans toutes les directions.
Le mouvement brownien hérite cependant de la marche aléatoire simple une propriété fondamentale : l'évolution de sa trajectoire à partir d'un instant $t$ n'est pas influencée par ce qui s'est passé avant cet instant. Ce sont deux processus « amnésiques », qui satisfont ce que l'on appelle la propriété de Markov. (Un exemple de déplacement aléatoire qui ne satisfait pas cette propriété est la marche aléatoire auto-évitante, qui ne revient jamais sur un site qu'elle a déjà visité.)
Théorèmes limites
La théorie des probabilités étudie de nombreux théorèmes dits « limites », dont les plus classiques sont
- la loi des grand nombres : si on tire un grand nombre de fois à pile ou face avec une pièce équilibrée, la proportion de « pile » est proche de la moitié avec probabilité proche de 1 ;
- le théorème central limite : l'écart entre le nombre de « pile » et sa moyenne théorique se comporte asymptotiquement comme la racine carrée du nombre de jets multipliée par une loi normale (une illustration de ce théorème central limite est donnée par la planche de Galton).
La convergence de la marche aléatoire vers le mouvement brownien après changement d'échelle est un cas particulier de principe d'invariance : une classe de théorèmes limites qui peut s'interpréter comme une généralisation du théorème central limite pour des trajectoires aléatoires.
Retour à la case départ
Une question fondamentale dans l'étude de processus comme la marche aléatoire est de savoir avec quelle probabilité la trajectoire repasse par son point de départ. Dans le cas de la marche aléatoire dans le plan présentée sur notre animation, on revient une infinité de fois au point de départ avec probabilité 1 : on dit que cette marche est récurrente. C'est aussi le cas si l'on considère la marche aléatoire en dimension 1 (avec probabilité $1/2$ on se déplace d'une case vers la droite ou vers la gauche). En revanche, si on se place en dimension 3 (le déplacement se fait dans les trois direction, il y a à chaque étape 6 pas possibles de même probabilité), la probabilité que l'on ne revienne jamais au point de départ est strictement positive. On parle alors de marche aléatoire transiente.
Aller à l'animation sur la marche aléatoire et le mouvement brownien.