Comment on allume la flamme olympique

La tradition veut que la flamme olympique soit allumée par le soleil lui-même, grâce à l'utilisation d'un objet connu depuis l'antiquité : le miroir parabolique. La forme particulière de ce miroir lui confère une propriété remarquable : si son axe est dirigé vers le soleil, tous les rayons lumineux arrivant sur sa surface sont renvoyés dans la direction d'un même point, le foyer. Un matériau inflammable placé en ce foyer est exposé à une telle concentration d'énergie solaire qu'il s'enflamme rapidement.
Plus précisément, la forme géométrique du miroir utilisé est un paraboloïde de révolution, obtenu en faisant tourner une courbe plane appelée parabole autour de son axe de symétrie. Nous proposons de présenter ci-dessous les propriétés géométriques de la parabole sur lesquelles est basé le fonctionnement du miroir parabolique.
Qu'est-ce qu'une parabole ?
Il existe plusieurs manières, toutes équivalentes bien sûr, de définir une parabole. Celle que nous présentons ici est très classique : elle s'obtient à partir d'une droite $\mathcal{D}$ appelée directrice et d'un point $F$ pris en-dehors de $\mathcal{D}$, appelé foyer. Dans les figures qui suivront, la directrice $\mathcal{D}$ sera toujours représentée horizontalement, et le foyer $F$ situé au-dessus de la directrice. Cette configuration correspond au cas où les rayons du soleil sont verticaux.
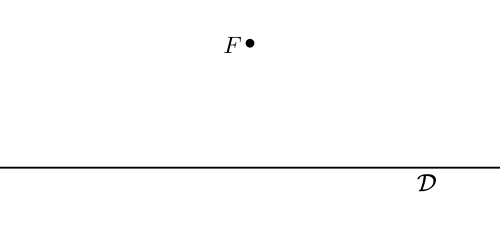
Pour un point $M$ quelconque du plan, on peut comparer la distance $d(M,F)$ qui le sépare du foyer et la distance $d(M,\mathcal{D})$ qui le sépare de la directrice (c'est-à-dire la distance entre $M$ et sa projection orthogonale sur $\mathcal{D}$). Ceci permet de distinguer deux régions du plan :
- celle où $d(M,\mathcal{D})\lt d(M,F)$ (c'est le cas du point $M_1$ sur la figure ci-dessous : on constate que le cercle de centre $M_1$ passant par $F$ coupe $\mathcal{D}$ en deux points) ;
- celle $d(M,\mathcal{D})\gt d(M,F)$ (c'est le cas du point $M_2$ sur la figure, on constate que le cercle de centre $M_2$ passant par $F$ ne rencontre pas $\mathcal{D}$).
La frontière entre ces deux régions est une courbe, formée de tous les points du plan qui sont exactement à la même distance du foyer $F$ et de la directrice $\mathcal{D}$ : cette courbe est la parabole de foyer $F$ et de directrice $\mathcal{D}$. Le point $P$ sur la figure est situé sur la parabole : le cercle de centre $P$ passant par $F$ est tangent à cette droite, c'est-à-dire qu'il ne touche la droite $\mathcal{D}$ qu'en un seul point (la projection orthogonale de $P$ sur $\mathcal{D}$), et donc $d(P,F)=d(P,\mathcal{D})$.
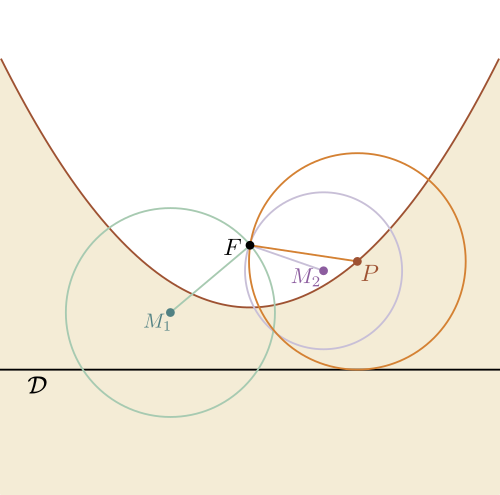
La parabole de foyer $F$ et de directrice $\mathcal{D}$ est l'ensemble des points du plan à égale distance de $F$ et de $\mathcal{D}$. Au-dessus de la parabole, les points sont plus près de $F$, en-dessous de la parabole ils sont plus près de $\mathcal{D}$. Vous pouvez visualiser ceci en déplaçant le pointeur de la souris sur l'image ci-dessus : le cercle centré sur le pointeur et passant par $F$ est tracé automatiquement, ce qui permet de voir si le pointeur est plus près ou plus loin du foyer que de la directrice.
Réflexion, tangente et symétrie
Pour décrire la manière dont un rayon de soleil vertical qui vient toucher la parabole en un point $P$ est réfléchi, il faut introduire la tangente à la parabole en $P$ : c'est la droite $\mathcal{T}$ qui ne touche la parabole qu'au seul point $P$, tous les autres points de cette droite étant en-dessous de la parabole. En général, identifier la tangente à une courbe nécessite de recourir au calcul différentiel. Mais dans le cas de la parabole, il suffit de simples arguments géométriques.
![La médiatrice de [FH] est la tangente à la parabole en P](MGPH.png)
En effet, pour un point $P$ fixé sur la parabole, construisons son projeté orthogonal $H$ sur la directrice $\mathcal{D}$. On a alors, puisque $P$ est sur la parabole $$ d(P,F) = d(P,\mathcal{D}) = d(P,H). $$ Soit $\mathcal{T}$ la médiatrice du segment $[FH]$ : l'égalité ci-dessus montre que la droite $\mathcal{T}$ passe par $P$. De plus, pour tout point $M$ sur la médiatrice $\mathcal{T}$, on a également $$ d(M,F) = d(M,H). $$ Fixons un tel point $M$ sur $\mathcal{T}$, et notons $G$ le projeté orthogonal de $M$ sur la directrice $\mathcal{D}$. On vérifie en utilisant le théorème de Pythagore dans le triangle rectangle $MGH$ que $$ d(M,G) \leq d(M,H), $$ avec égalité si et seulement si $G=H$, c'est-à-dire lorsque $M=P$. Or, le membre de gauche de l'inégalité est la distance de $M$ à la directrice $\mathcal{D}$, tandis que le membre de droite, comme on l'a vu, est aussi la distance de $M$ au foyer $F$. On en déduit que tout point $M$ de $\mathcal{T}$ qui est différent de $P$ vérifie $$ d(M,\mathcal{D}) \lt d(M,F), $$ ce qui prouve que tous les points de $\mathcal{T}$ autres que $P$ sont situés strictement sous la parabole. Ainsi la médiatrice $\mathcal{T}$ de $[FH]$ est la tangente en $P$ à la parabole.
On peut reformuler le résultat ci-dessous ainsi :
Pour tout point $P$ de la parabole, son projeté orthogonal $H$ sur la directrice $\mathcal{D}$ est le symétrique du foyer $F$ par rapport à la tangente $\mathcal{T}$ à la parabole en $P$.
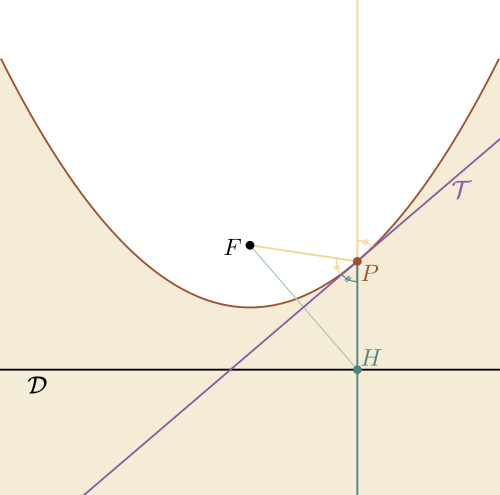
Pour un rayon de soleil vertical qui vient toucher la parabole au point $P$, tout se passe comme si la parabole était confondue avec la tangente $\mathcal{T}$. Les lois de la réflexion stipulent alors que le rayon de soleil réfléchi forme avec la tangente un angle de même mesure que le rayon vertical incident qui arrive en $P$. De manière équivalente : la trajectoire prise par le rayon réfléchi est la symétrique par rapport à la tangente $\mathcal{T}$ de celle qu'il aurait suivie s'il n'avait pas rencontré la parabole. Le résultat établi ci-dessus prouve alors que le rayon réfléchi passe par le foyer $F$, et ceci pour tout point $P$ de la parabole !
Une mise en plis parabolique
En pliant une feuille de papier, on peut visualiser concrètement le fait que la tangente à la parabole en $P$ soit toujours la médiatrice du segment $[FH]$, où $F$ est le foyer et $H$ la projection orthogonale de $P$ sur la directrice.

On part d'une feuille de papier sur laquelle on a marqué un point $F$, le foyer. La directrice est matérialisée par le bord inférieur de la feuille. Sur cette directrice on trace des points à intervalles réguliers, et on trace les mêmes points de la directrice de l'autre côté de la feuille.

Pour chaque point $H$ tracé sur la directrice, on marque le pli qui le rabat sur le foyer $F$ : ce pli matériatlise la médiatrice du segment $[FH]$ et c'est donc une tangente à la parabole.

Lorsque tous les plis sont marqués, on voit la parabole de foyer $F$ et de directrice le bord de la feuille se matérialiser.

On dit que la parabole est l'enveloppe des médiatrices des segments $[FH]$ lorsque $H$ parcourt la directrice.