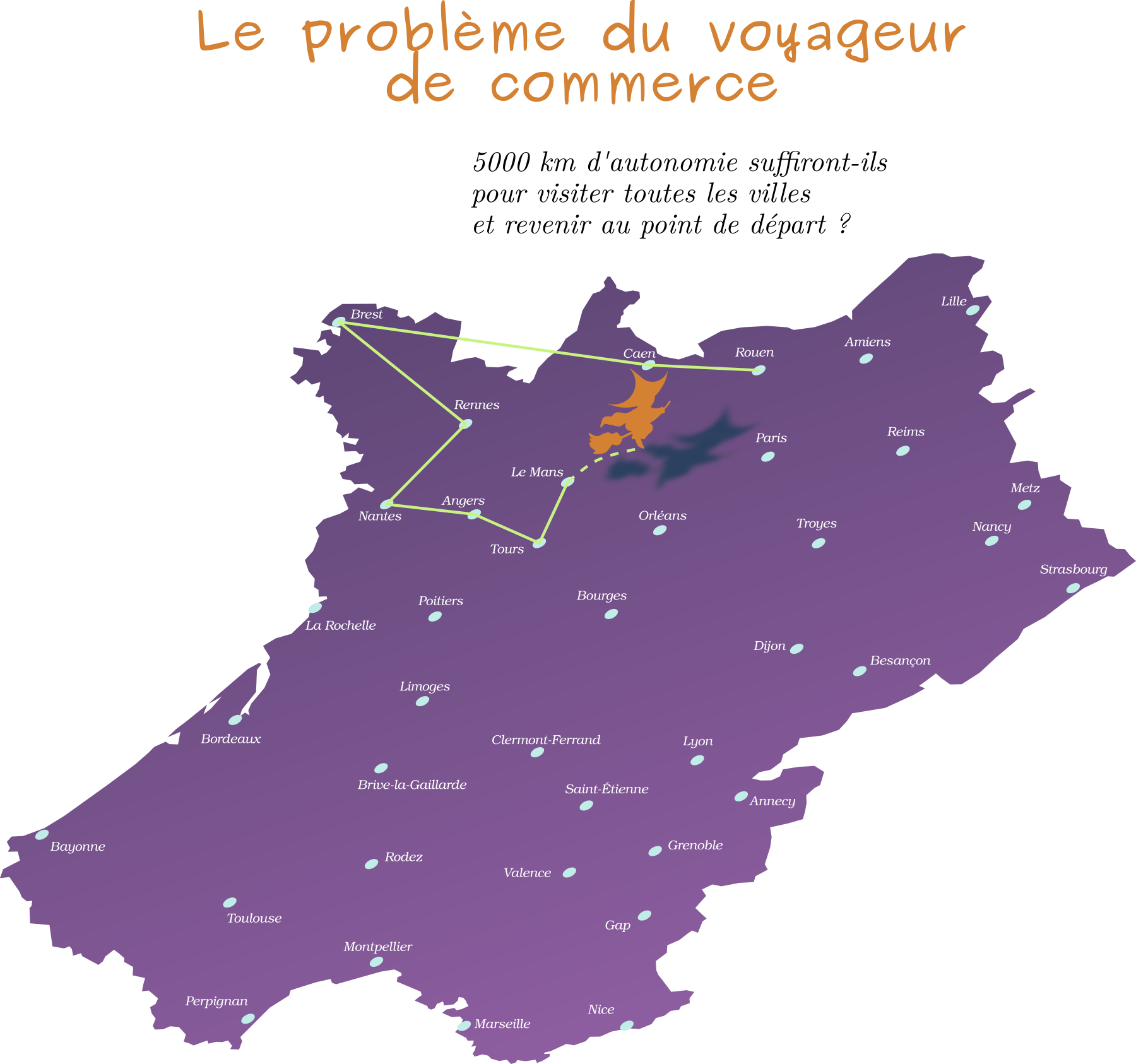
Un sorcier voyageur part de Rouen pour effectuer un tour de France durant lequel il doit visiter les 39 autres villes indiquées sur la carte, et revenir à son point de départ. L'objectif est de déterminer l'ordre dans lequel il effectue son parcours afin de minimiser la longueur totale du circuit effectué.

Sur son balai volant électrique, il n'a pas à s'embarrasser à suivre les routes (il peut même si besoin passer au-dessus de la mer), et la distance parcourue entre deux villes est mesurée à vol d'oiseau. Cependant, l'autonomie de son balai étant de 5000 km, il voudrait savoir si il peut se dispenser d'emmener avec lui son chargeur.

Pour l'aider à répondre à cette question, et à trouver le plus court circuit possible, vous pouvez :

• Choisir l'ordre dans lequel il effectue son parcourt, en cliquant successivement sur les villes dans l'ordre de la visite,
• ou bien vous en remettre au hasard et tirer au sort un circuit, en cliquant sur le bouton .

La longueur totale du circuit est donnée dans le cadre correspondant. Pour essayer d'améliorer le circuit, deux options sont possibles :

• appliquer un algorithme de descente, qui à chaque itération tente de réduire systématiquement la longueur du circuit en effectuant de petites modifications (bouton  )
• ou bien utiliser l'algorithme appelé « recuit simulé » (bouton  ), qui à la différence de l'algorithme de descente peut accepter de temps en temps de rallonger la longueur du circuit.

Dans le cas du recuit simulé, le dernier circuit affiché n'est pas nécessairement le meilleur trouvé : pour visualiser le plus court circuit obtenu au cours de l'exécution de l'algorithme, cliquer sur le bouton .

La courbe à droite de la carte indique l'évolution de la longueur de circuit au fur et à mesure des étapes d'exécution des deux algorithmes. Les barres verticales indiquent les instants où le recuit simulé fait augmenter la longueur du circuit.

Pour en savoir plus sur ce problème, connu sous le nom du « problème du voyageur de commerce », et sur les algorithmes de descente et du recuit simulé utilisés ici, voir cette page.