La suite des nombres de Fibonacci commence par $$1,\,1,\,2,\,3,\,5,\,8,\,13,\,21,\,34,\,55,\,89$$ et se poursuit indéfiniment en répétant toujours la même règle : chaque nouveau nombre (à partir du troisième) est la somme des deux précédents. En notant $F_n$ le $n-$ième terme de la suite, pour $n\geq1$ un nombre entier, la relation de récurrence qui définit la suite de Fibonacci est $$F_{n+2}=F_{n+1}+F_n.$$ Connue notamment pour ses liens avec le mythique nombre d'or, $$\varphi=\frac{1+\sqrt5}{2},$$ cette suite a été introduite par le mathématicien italien Léonard de Pise (dont le surnom était Fibonacci). Elle a de fabuleuses propriétés mathématiques, et ses termes apparaissent étonnamment dans la nature, en comptant les spirales formées sur certains végétaux ou les pétales des fleurs. Nous regroupons ici quelques documents et activités autour de cette suite.
Trois tours de magie
fondés sur les propriétés de la suite de Fibonacci :
- Une addition fibomagique : calculer la somme de deux nombres alors qu'on ne connaît qu'un seul de ces deux nombres !
- Un tour de cartes pour deviner un nombre secret en utilisant la décomposition des nombres entiers en somme de nombres de Fibonacci (appelée décomposition de Zeckendorf, et expliquée ici).
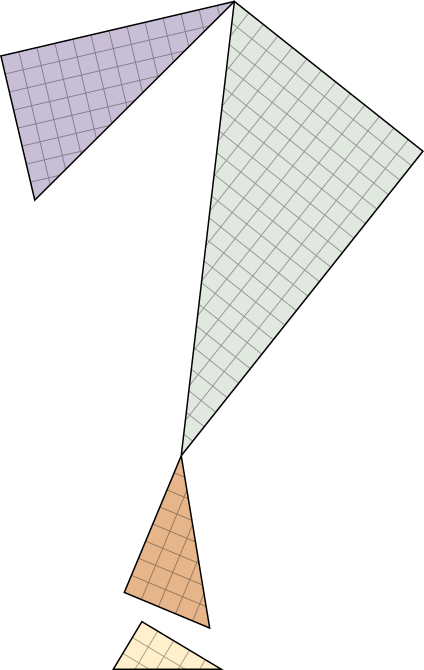
- Des triangles carrément magiques ! Les nombres de Fibonacci permettent de construire des triangles aux propriétés mystérieuses...

Les nombres de Fibonacci et le nombre d'or dans la nature

- Les nombres de Fibonacci au jardin : retrouvez les nombres de Fibonacci dans les spirales formées par certains végétaux.
- Dénichez le nombre d'or au cœur des fleurs : une application pour jouer avec un modèle de formation de certains végétaux (cœur d'une fleur de tournesol...), et comprendre en quoi le nombre d'or y joue un rôle essentiel.

- Des explications sur le modèle et le rôle du nombre d'or.


Deux posters
à télécharger dans notre collection : Magie des nombres de Fibonacci, et Fibonacci au jardin.