Un problème simple ?
L'énoncé du problème est simple : un voyageur doit se rendre dans un certain nombre de villes et revenir à son point de départ. Il souhaite déterminer l'ordre dans lequel il visite les villes de sorte à parcourir la plus petite distance totale.
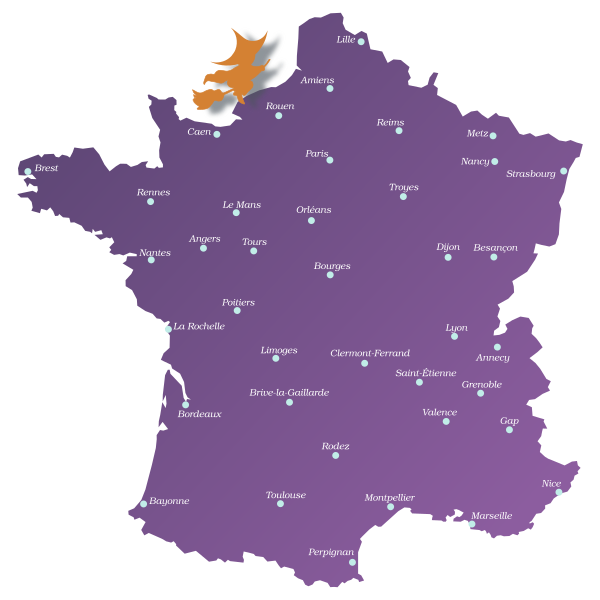
Dans cet exemple reprenant la situation de notre animation, un sorcier part de Rouen et cherche à visiter les 39 autres villes sur la carte avant de revenir à son point de départ. Comme il se déplace sur un balai volant, la distance entre deux villes étapes est mesurée à vol d'oiseau. Mais son balai électrique n'a qu'une autonomie de 5 000 km. Peut-il parcourir toutes les villes et revenir à son point de départ sans avoir à le recharger ?
Il n'y a qu'un nombre fini de circuits possibles, et donc parmi eux il y en a au moins un dont la longueur totale est minimale. Il est même facile d'écrire un programme informatique qui liste tous les circuits parcourant ces villes, calcule pour chacun d'eux la distance parcourue, et renvoie à la fin celui qui a la plus petite longueur.
Explosion combinatoire
Mais combien de temps un tel programme mettrait pour donner le résultat ? Notons $n$ le nombre de villes à visiter (y compris la ville de départ, qui est aussi la ville d'arrivée, et qui est déterminée par le lieu où se trouve déjà le voyageur). Pour choisir sa première étape, le voyageur dispose de $(n-1)$ options qui correspondent aux $(n-1)$ villes différentes de la ville de départ. Une fois déterminée cette première étape, il y a encore $(n-2)$ choix possibles pour la deuxième ville à visiter (qui doit être différente de la ville de départ et de la première destination), puis $(n-3)$ pour la troisième et ainsi de suite. Pour l'étape $(n-2)$, il reste deux villes possibles pour le voyageur, et pour l'étape $(n-1)$ il ne lui reste qu'une seule ville à visiter avant de revenir à son point de départ. Le nombre total de circuits possibles pour parcourir les $n$ villes en partant d'une ville initiale donnée est donc égal au produit $$ (n-1)\times(n-2)\times(n-3) \times\cdots\times 2 \times 1, $$ que l'on note généralement $(n-1)!$, et qui se lit « factorielle $(n-1)$ ».
Mais en fait, on n'a pas besoin d'examiner tous ces circuits, car chacun d'entre eux a évidemment la même longueur que son symétrique : celui obtenu en parcourant les villes dans l'ordre exactement inverse. Il reste donc, en fait, « seulement » $(n-1)!/2$ circuits à considérer, ce qui est égal au produit $$ (n-1)\times(n-2)\times(n-3) \times\cdots\times 4 \times 3. $$
Si on a 10 villes à visiter, le nombre de circuits à examiner vaut donc $$ 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 = 181\,440. $$ Si on dispose d'un ordinateur assez puissant pour traiter un million de circuits par seconde, il s'en sortira donc en environ 18 centièmes de seconde. Mais si on veut visiter 20 villes, un calcul analogue montre que le même ordinateur aura cette fois besoin de 1 929 ans pour examiner tous les circuits ! Pour 30 villes, le temps nécessaire est de l'ordre de 10 millions de fois l'âge estimé de l'univers... Dans l'application mise en ligne sur notre site, il y a 40 villes ; vous pouvez vous amuser à estimer la durée d'exécution de l'algorithme dans ce cas.
À cause de ce phénomène, que l'on appelle l'explosion combinatoire, cette approche naïve qui consiste à regarder tous les circuits possibles n'est absolument pas réalisable en pratique. Et malheureusement, on ne connaît pas d'autre algorithme qui donnerait la meilleure solution en un temps raisonnable, ni même qui répondrait à coup sûr à une question du style « existe-t-il un circuit parcourant toutes les villes et dont la longueur est inférieure à 5 000 km ?». On en est réduit à utiliser des méthodes d'optimisation qui n'explorent que partiellement l'ensemble des configurations possibles, et ne donnent donc que des solutions approchées.
Algorithme de descente
On peut se représenter la recherche du plus court circuit comme l'exploration d'un paysage montagneux complexe, avec des pics, des vallées et des cols. Ce paysage est constitué de l'ensemble de tous les circuits possibles, et l'altitude d'un point correspond à la longueur totale du circuit auquel correspond ce point. Le problème du voyageur de commerce revient alors à la recherche du point le plus bas de ce paysage. Imaginons un randonneur perdu dans le brouillard, sans carte ni GPS au milieu de ces montagnes. Pour regagner la vallée, une stratégie naturelle consiste pour lui à avancer un peu au hasard, mais en n'effectuant que des pas qui vont dans le sens de la descente. Chaque pas lui faisant perdre un peu d'altitude, il avance jusqu'à se trouver dans une position où toutes les directions autour de lui le feraient remonter. Il arrive ainsi à un minimum local, c'est-à-dire un point du paysage dont l'altitude est plus basse que celle de tous les autres points autour de lui.
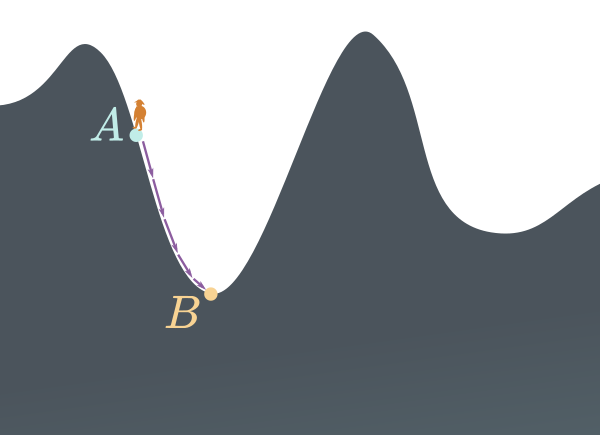
Si par exemple le randonneur applique l'algorithme de descente à partir du point $\small A$, il va aboutir au minimum local situé en $\small B$ où l'algorithme stoppera, puisqu'il ne peut pas partir de $\small B$ sans augmenter à nouveau l'altitude.
Dans le cas du problème du voyageur de commerce, voilà comment se traduit l'algorithme de descente : on part d'un circuit quelconque, que l'on essaye d'améliorer par petites modifications successives. On peut par exemple choisir un circuit voisin aléatoirement, en prenant au hasard deux étapes du circuit et en les « échangeant », comme expliqué sur le schéma ci-dessous.
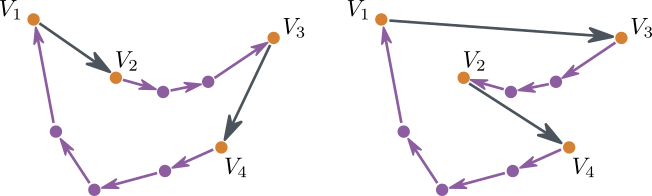
Une modification élémentaire d'un circuit, qui est l'analogue d'un pas du randonneur. On choisit au hasard deux étapes qui font parties du circuit (une d'une ville $\small V_1$ à une ville $\small V_2$, et l'autre d'une ville $\small V_3$ à une ville $\small V_4$, et on les remplace par deux autres étapes, allant de $\small V_1$ à $\small V_3$ et de $\small V_2$ à $\small V_4$. On change aussi le sens de toutes les étapes entre $\small V_2$ et $\small V_3$.
Le principe de l'algorithme de descente consiste à ne valider ce changement élémentaire que si le nouveau circuit est de longueur totale inférieure à celle de l'ancien circuit. En répétant cette opération, la longueur du circuit ne peut que décroître, et elle finit par se stabiliser pour un circuit qui a une longueur plus petite que tous les circuits voisins. (Ici on dit que deux circuits sont voisins si on peut passer de l'un à l'autre par une modification élémentaire de la forme de celle décrite ci-dessus.)
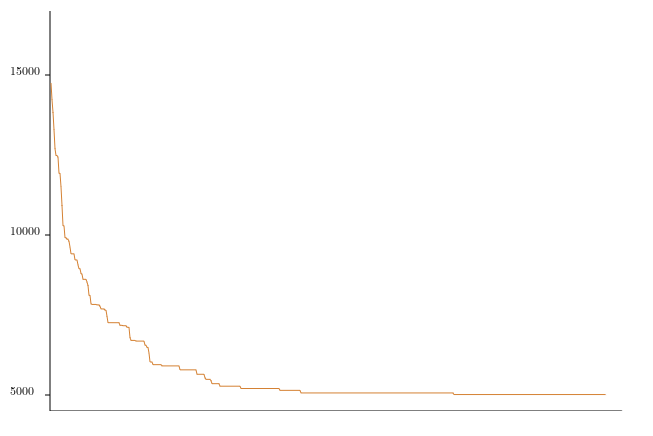
Ce graphique montre l'évolution de la longueur du circuit en fonction du nombre d'itérations de l'algorithme de descente.
Le minimum local où termine l'algorithme de descente a toutes les raisons d'être meilleur que le point de départ, cependant le fait d'y rester bloqué empêche l'exploration d'autres portions du paysage où on pourrait trouver d'autres points d'altitude encore moins grande.
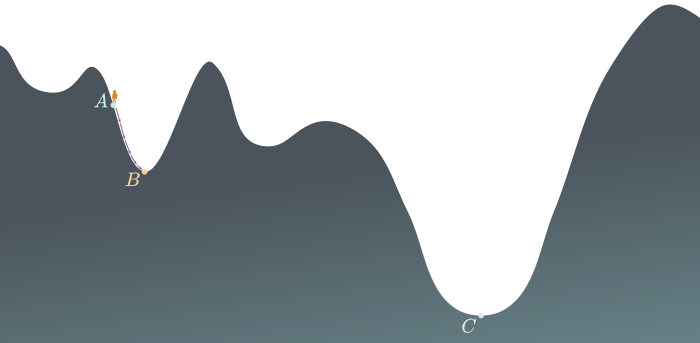
L'algorithme de descente restant bloqué au minimum local situé en $\small B$, on ne verra pas la configuration bien meilleure en $\small C$.
L'algorithme du recuit simulé
Pour ne pas rester piégé dans les minimums locaux et se laisser la possibilité d'explorer tout le paysage, on comprend bien qu'il faut de temps en temps accepter de remonter la pente, c'est-à-dire augmenter parfois la longueur du circuit. C'est ce que propose l'algorithme du recuit simulé. Son principe reste proche de l'algorithme de descente : on cherche à améliorer progressivement le circuit en effectuant des modifications élémentaires. Si une modification élémentaire fait baisser la longueur du circuit, comme précédemment on l'adopte automatiquement. La différence réside dans la façon de traiter les modifications qui font augmenter la longueur du circuit : si une itération de l'algorithme propose de passer d'un circuit de longueur $L_1$ à un nouveau circuit de longueur $L_2>L_1$, cette fois on décide aléatoirement d'accepter le nouveau circuit avec une probabilité égale à $$ \exp\bigl(-(L_2-L_1)/T\bigr), $$ où $T$ est un paramètre positif appelé la température. Des propriétés de la fonction exponentielle utilisée dans cette formule, il découle qu'à température fixée, la probabilité d'accepter le nouveau circuit décroit très vite vers 0 lorsque $L_2-L_1$ devient grand. Plus l'augmentation de longueur du circuit est grande, plus la probabilité d'accepter le changement est faible. De même, plus la température $T$ est proche de 0, plus il est difficile d'accepter un nouveau circuit de longueur plus grande.
Itérer cette procédure à température fixée revient à appliquer ce qui s'appelle l'algorithme de Metropolis-Hastings. L'étude théorique de cet algorithme, qui est un cas particulier de chaîne de Markov homogène, montre qu'en répètant l'opération un grand nombre de fois, la probabilité d'obtenir un circuit donné de longueur $L$ devient proportionnelle à $\exp(-L/T)$. Ainsi les circuits les moins longs sont les plus probables. Et plus le paramètre $T$ représentant la température est proche de 0, plus la distribution du circuit obtenu se concentre sur les circuits de longeur minimum.
L'algorithme du recuit simulé, inventé par trois chercheurs d'IBM en 1 983 (Kirkpatrick, Gelatt et Vecchi), et indépendamment par Černy en 1 985, se base donc sur celui de Metropolis-Hastings. Mais au lieu de garder la température fixée, on fait décroître très lentement le paramètre $T$ vers 0. (On obtient alors une chaîne de Markov inhomogène, dont les probabilités de transition évoluent au cours du temps.) Ainsi au début de l'exécution de l'algorithme on s'échappe assez facilement des minimums locaux, mais après un grand nombre d'itérations cela devient de plus en plus difficile.
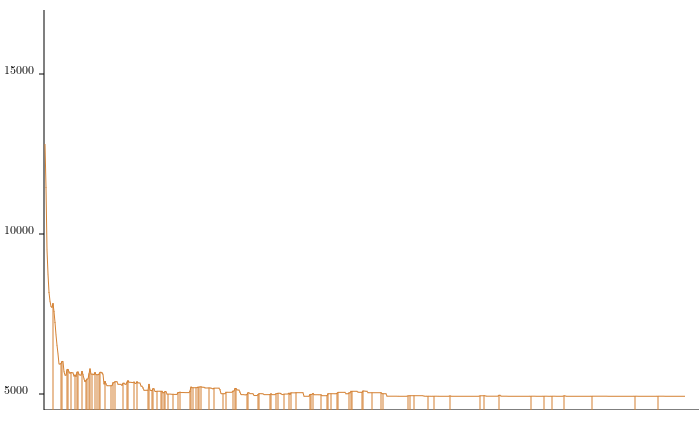
Ce second graphique montre l'évolution de la longueur du circuit en fonction du nombre d'itérations dans le cas de l'algorithme du recuit simulé. Les barres verticales correspondent aux instants où la longueur du circuit augmente. Il y en a plus au début de l'exécution (température élevée) qu'à la fin (température basse).
Le nom de l'algorithme, le recuit simulé, fait référence à un procédé de métallurgie qui consiste à chauffer un métal à haute température et à le refroidir lentement, ce qui confère au matériau une structure cristalline plus stable et améliore ses propriétés physiques.

L'algorithme du recuit simulé a l'avantage d'être très simple à programmer, et facile à adapter à de nombreux problèmes d'optimisation. La principale difficulté est, comme en métallurgie, de trouver la bonne façon de faire décroître la température. L'étude théorique montre qu'on est presque sûr d'arriver à un minimum global si $T$ décroît suffisamment lentement ($T \leq K/\log n$, où $n$ représente le nombre d'itérations, et $K$ est une constante dépendant du problème traité). Mais cette décroissance est trop lente pour être appliquée en pratique. On utilise plutôt des schémas de refroidissements du type $T = T_0\theta^n$, où $\theta$ est un nombre légèrement inférieur à 1. On n'arrive en général qu'à un minumum local, que l'on espère assez proche du minimum global. Cependant l'espace des circuits possibles étant tellement gigantesque et complexe, la longueur du meilleur circuit trouvé en ne faisant tourner l'algorithme que quelques minutes peut beaucoup varier en fonction du circuit initial et de l'aléa utilisé au cours de l'exécution.
Aller à l'animation sur le problème du voyageur de commerce.
Voir aussi notre poster sur le problème du voyageur de commerce.