Des couloirs plus ou moins longs
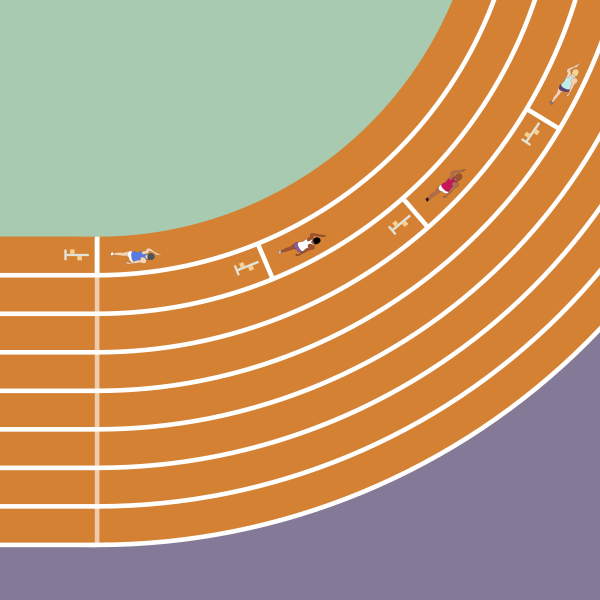
En athlétisme, la course du 400 mètres correspond à un tour complet de piste. Mais ceci n'est exact que pour le couloir numéro 1, celui qui est le plus à la corde : si on effectue un tour de piste sur un autre couloir, la distance parcourue augmente à mesure que l'on s'éloigne du centre du stade. C'est pour compenser cette différence de longueur que les départs des coureurs du 400 mètres sont décalés les uns par rapport aux autres. Mais comment calcule-t-on le décalage entre deux couloirs ?
Le tour de piste complet comporte deux sections en ligne droite et deux demi-cercles. La longueur des lignes droites ne varie pas avec le couloir, mais bien sûr celle des deux demi-cercles augmente quand on s'éloigne du centre. La contribution de ces deux demi-cercles correspond au périmètre d'un cercle entier, soit $2\pi R$ en notant $R$ le rayon. Lorsque l'on passe d'un couloir au couloir suivant, le rayon augmente exactement de la largeur $L$ d'un couloir (qui en pratique vaut 1,22m sur une piste d'athlétisme). L'augmentation de la longueur d'un tour complet entre un couloir et le suivant vaut donc $$ 2\pi(R+L)-2\pi R = 2\pi L. $$ Pour compenser cette augmentation les starting-blocks sont eux-mêmes décalés de $2\pi L$ d'un couloir à l'autre, soit 7,67m.

De quoi dépend le décalage des starting-blocks ?
On peut formuler deux remarques sur le calcul ci-dessus :
- Le décalage dépend de la largeur des couloirs, mais pas de la longueur de la piste : si on construisait les stades avec un tour complet de 800 mètres, ou même de 5000 mètres, le décalage pour une course d'un tour complet serait le même, pourvu que les couloirs conservent la même largeur.
- Le calcul du décalage ne faisant intervenir que les portions semi-circulaires, il ne changerait pas si on faisait varier la longueur des portions en ligne droite, et même à la limite si le stade était parfaitement circulaire.

Et si on changeait la forme du stade ?
La deuxième remarque nous conduit à poser la question suivante : comment calculerait-on le décalage pour d'autres formes de stade ?
Par exemple, on pourrait imaginer un stade de type « triangulaire », comportant trois portions en ligne droite reliées par des arcs de cercles centrés aux sommets d'un triangle équilatéral, comme sur la figure qui suit.

Comme sur un stade standard, la longueur des portions en ligne droite ne varie pas avec le couloir, et si on met bout à bout les trois arcs de cercles, on retrouve un cercle entier. Le même raisonnement aboutit à la même conclusion : le décalage d'un couloir à l'autre doit à nouveau être de $2\pi L$, avec $L$ la largeur d'un couloir.
En poursuivant la même idée, on peut imaginer des formes plus complexes de stade, où la piste est toujours formée de portions en ligne droite reliées par des arcs de cercles centrés sur les sommets d'un polygone convexe.

À nouveau le même raisonnement s'applique, car les portions en arc de cercle mises bout à bout forment toujours un cercle complet, tandis que la contribution des portions en ligne droite ne changent pas d'un couloir à l'autre. Le décalage du départ entre deux couloirs successifs doit donc toujours être $2\pi L$.
En y réfléchissant un peu, l'utilisation du coefficient $2\pi$ ici n'est pas surprenante puisque les parties courbes des différents modèles de stade présentés ci-dessus sont toujours des arcs de cercles, et mis bout à bout ils forment un cercle entier.
Mais comment devrait-on calculer le décalage entre les couloirs si la forme du stade était encore beaucoup plus complexe, comme sur l'image ci-dessous où aucune partie ne correspond ni à une ligne droite ni à un arc de cercle ?

La même formule pour toutes les formes de stade !
Étrangement, le calcul effectué dans les configurations de stade où les courbes sont des arcs de cercles continue à être valable pour des formes beaucoup plus générales : dès que les couloirs ont une largeur constante égale à $L$, la longueur d'un tour complet entre un couloir et le suivant augmente toujours de $2\pi L$, même si la forme n'a rien à voir avec un cercle !
Nous allons esquisser une preuve de cet énoncé lorsque le stade a une forme convexe quelconque, en nous basant sur un argument de Joseph-Émile Barbier. Le raisonnement de Barbier permet de relier la longueur $a$ d'une courbe plane au résultat moyen d'une expérience aléatoire qui est une variation du problème des aiguilles de Buffon : on considère une courbe plane, figurée par une nouille ou un fil de fer, que l'on jette au hasard sur un parquet dont toutes les lames ont une largeur égale à $L$. On note $\mathcal{E}$ le nombre moyen d'intersections entre la courbe et les rainures du parquet. Alors $\mathcal{E}$ est relié à la longueur $a$ de la courbe par la formule de Barbier : $$ \mathcal{E} = \frac{2a}{\pi L}. $$ (voir notre page d'explications sur les aiguilles de Buffon.)
Appliquons cela à une courbe plane fermée $\gamma$ qui délimite une partie convexe du plan, ainsi qu'à la courbe $\gamma'$ dessinée autour de $\gamma$ à une distance constante égale à $L$ : $\gamma$ et $\gamma'$ représentent les trajets de deux coureurs dans deux couloirs successifs de la piste. Le même paramètre $L$ est utilisé pour la largeur des lames du parquet et la largeur du couloir, et on jette ensemble au hasard ces deux courbes sur le parquet.
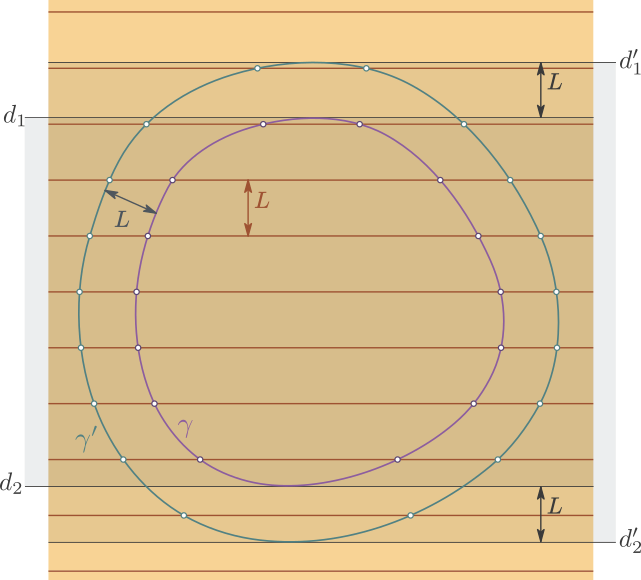
Nous allons comparer les nombres d'intersections de $\gamma$ et $\gamma'$ avec les rainures du parquet, notés respectivement $N$ et $N'$. Commençons par construire les deux droites $d_1$ et $d_2$ qui sont parallèles aux lames du parquet, qui touchent la courbe $\gamma$ mais de telle façon que $\gamma$ soit située entre $d_1$ et $d_2$. La probabilité que l'une des rainures du parquet coïncide avec $d_1$ ou $d_2$ est nulle, donc on peut supposer que ce n'est pas le cas. Alors, grâce à l'hypothèse de convexité, chaque rainure du parquet qui est entre $d_1$ et $d_2$ coupe $\gamma$ en exactement 2 points.
On construit de même les droites $d'_1$ et $d'_2$ entre lesquelles est coincée la courbe $\gamma'$. Chaque rainure du parquet entre $d'_1$ et $d'_2$ rencontre également $\gamma'$ en exactement 2 points. Or, la distance entre $d_1$ et $d'_1$ vaut $L$, donc il y a exactement une rainure supplémentaire entre $d_1$ et $d'_1$. De même il y a exactement une rainure supplémentaire entre $d_2$ et $d'_2$. On en conclut que $$ N'= N + 4. $$ Par conséquent, les moyennes respectives $\mathcal{E}$ et $\mathcal{E}'$ de $N$ et $N'$ vérifient la même relation : $$ \mathcal{E}' = \mathcal{E} + 4. $$ En utilisant la formule de Barbier ci-dessus, on en déduit que les longueurs respectives $a$ et $a'$ de $\gamma$ et $\gamma'$ satisfont $$ a' = \frac{\mathcal{E}'\pi L}{2} = \frac{(\mathcal{E}+4)\pi L}{2} = a + 2\pi L. $$
Enfin, pour ceux qui voudraient se convaincre que la même formule reste vraie dans un cadre très général, même lorsque la forme du stade n'est pas convexe, nous renvoyons par exemple à cet article (en anglais).