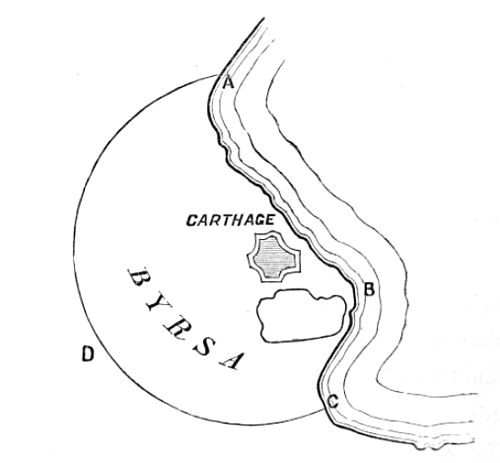
La légende de la fondation de Carthage par Didon

Didon était une princesse de l'Antiquité qui fut obligée de s'exiler loin de ses terres natales à cause de graves problèmes familiaux. Elle traversa la mer Méditerranée sur un bateau accompagnée d'une suite importante, et débarqua sur les côtes de l'actuelle Tunisie. Elle demanda au roi local de lui accorder une terre où elle pourrait fonder une cité. Le roi lui accorda de prendre autant de terre qu'elle voudrait, tant qu'elle pourrait la faire tenir dans la peau d'un bœuf. Didon entreprit de faire découper la peau du bœuf en très fines bandes, qu'elle mit bout à bout afin d'obtenir une très longue lanière. Il lui restait alors à disposer cette lanière de sorte à entourer un territoire le plus grand possible. Mais quelle forme donner à cette lanière pour que l'aire délimitée soit maximum ? Voilà ce qui s'appelle un problème isopérimétrique : parmi toutes les figures planes qui peuvent être délimitées par cette lanière de longueur fixée (donc qui ont un périmètre donné), quelle est celle dont la surface est la plus grande ?
Le problème isopérimétrique classique dans le demi-plan
Dans cet exercice, Didon bénéficiait d'un avantage important, car elle pouvait également utiliser le bord de la mer comme délimitation « gratuite » pour la cité de Carthage. Il lui suffisait donc de relier deux points de la côte avec la lanière pour délimiter son territoire. En supposant pour simplifier que le bord de mer soit en ligne droite, comment relier deux points de la côte avec la lanière de longueur fixée de sorte à entourer la plus grande surface possible ?
Nous présentons ci-dessous les grandes lignes d'un argument assez élémentaire prouvant que la seule forme qui peut être solution du problème isopérimétrique dans le demi-plan est le demi-cercle. Autrement dit : si une courbe de longueur voulue maximise l'aire délimitée par la courbe et le bord de mer rectiligne, alors cette courbe est forcément un demi-cercle.

La première chose à remarquer est qu'une courbe solution doit forcément délimiter une partie convexe : si on tend un élastique autour de la forme délimitée, l'élastique doit suivre en tout point le contour. Ce n'est pas le cas sur la figure ci-dessus.

En effet une telle courbe ne peut pas maximiser la surface délimitée parmi toutes les courbes de même longueur, car en symétrisant la partie de la courbe dont l'élastique s'écarte, on obtient une nouvelle courbe de même longueur mais qui délimite un territoire plus grand.


Rentrons maintenant dans le cœur de l'argument. Supposons que la courbe ci-dessus soit notre championne, c'est-à-dire qu'elle délimite avec le bord de mer la plus grande surface possible parmi toutes les courbes de même longueur. On note $A$ et $B$ les points où la courbe touche la droite représentant le bord de la mer. On considère un point $M$ quelconque sur la courbe entre $A$ et $B$.
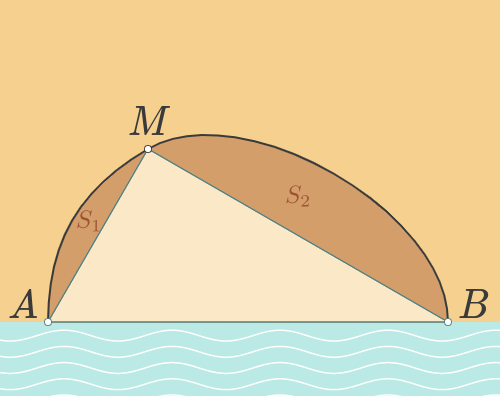
On découpe la surface délimitée par la courbe et le bord de mer en 3 parties : le triangle $AMB$, la partie au-dessus du segment $[AM]$ (dont on note $S_1$ l'aire) et la partie au-dessus du segment $[MB]$ (d'aire $S_2$). (Ici on utilise la convexité pour pouvoir dire que la courbe est bien située au-dessus des segments $[AM]$ et $[MB]$.)
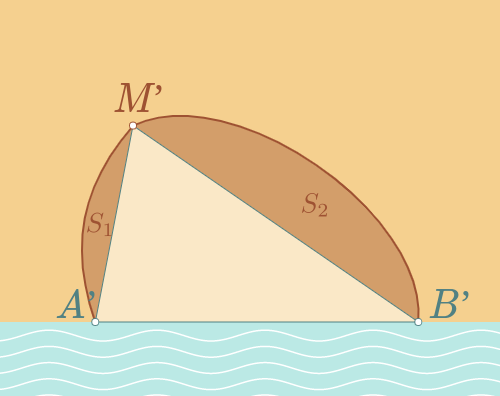
On peut alors jouer à construire d'autres courbes possibles : on commence par dessiner un nouveau triangle $A’M’B’$ où les points $A’$ et $B’$ sont aussi au bord de la mer, et tel qu'on ait les égalités de distances : $A’M’=AM$ et $B’M’=BM$. Puis on reporte au-dessus de $[A’M’]$ la partie de la courbe précédente qui était au-dessus de $[AM]$. On fait de même au-dessus du segment $[M’B’]$. On obtient une nouvelle courbe, qui relie les deux points du bord de mer $A’$ et $B’$, et dont la longueur est la même que la courbe initiale (elle est composée des deux mêmes morceaux qui ont juste été déplacés).
Cette fois l'aire sous la courbe est la somme de l'aire du triangle $A’M’B’$ et des deux mêmes surfaces $S_1$ et $S_2$. Mais rappelez-vous que la première courbe était la championne, donc ici l'aire doit être plus petite que précédemment. On en déduit : $$ \mbox{Aire}(AMB)\ge\mbox{Aire}(A’M’B’)$$ (puisque les autres morceaux sont identiques dans les deux cas).
Ainsi le triangle $AMB$ est aussi un champion dans son genre : parmi tous les triangles $A’M’B’$ dont les longueurs des côtés $A’M’$ et $M’B’$ sont fixées, il est celui d'aire maximum !
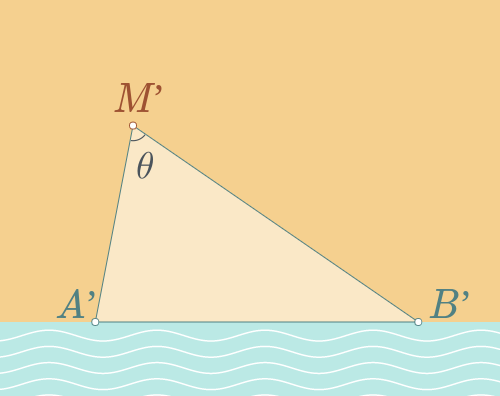
Or, il est facile de se convaincre que si les longueurs $A’M’$ et $M’B’$ sont fixées, la plus grande aire possible est obtenue lorsque le triangle est rectangle en $M’$. En effet si on note $\theta$ l'angle au sommet $M’$, l'aire du triangle $A’M’B’$ vaut $\frac{1}{2} A’M’\cdot M’B’\cdot \sin\theta$.
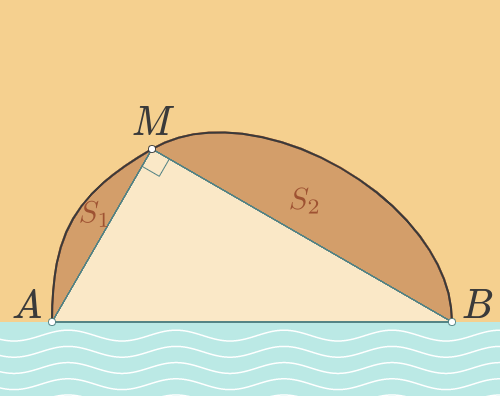
On en déduit que, sur la figure construite à partir de la courbe championne, le triangle $AMB$ est rectangle en $M$. Or, cette propriété caractérise le fait que $M$ soit situé sur le demi-cercle de diamètre $[AB]$. Mais cela étant valable pour tout point $M$ de la courbe championne, la conclusion est que cette courbe ne peut être que le demi-cercle !
Le problème isopérimétrique classique dans le plan
Quelle serait la forme optimum du contour tracé par Didon si celle-ci n'avait pas la possibilité d'utiliser le bord de mer comme frontière ? Autrement dit : quelle est dans le plan la courbe fermée de longueur fixée qui entoure la plus grande surface possible ? Là aussi, des arguments élémentaires permettent de se convaincre que si une courbe championne existe, elle ne peut être qu'un cercle, et cela en se ramenant au cas du demi-plan.
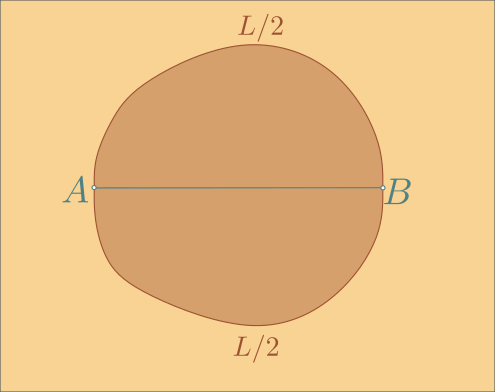
Supposons que la courbe ci-dessus soit meilleure que les autres pour le problème isopérimétrique dans le plan. On fixe un point $A$ arbitraire sur la courbe, puis on détermine le point $B$ de la courbe tel que la distance sur la courbe pour aller de $A$ à $B$ soit exactement la moitié de la longueur totale $L$. Alors l'aire délimitée par la courbe d'un côté de la droite $(AB)$ est forcément égale à celle délimitée par la courbe de l'autre côté. En effet, si ce n'était pas le cas on pourrait recopier en miroir la moitié de la courbe qui délimite la plus grande aire pour obtenir une nouvelle courbe de même longueur mais meilleure que notre supposée championne.
Puis on se convainc facilement que la partie de la courbe située au-dessus de la droite $(AB)$ est nécessairement une championne pour le problème isopérimétrique dans le demi-plan bordé par la droite $(AB)$. (Car si une meilleure courbe de même longueur existait dans ce demi-plan, on pourrait l'utiliser ainsi que sa symétrique pour obtenir une meilleure courbe de même longueur dans le plan.) C'est donc, d'après ce que nous avons vu précédemment, le demi-cercle de diamètre $[AB]$ situé au-dessus de $(AB)$. Et le même raisonnement prouve que l'autre moitié de la courbe est l'autre demi-cercle de diamètre $[AB]$. Et finalement notre courbe championne dans le plan est bien le cercle !
Les idées de la démonstration ci-dessus sont dues au mathématicien suisse Jacob Steiner (1848). Une vidéo reprenant cette démonstration est proposée dans la collection Les 5 min Lebesgue.
Mais notez bien que cet argument élémentaire ne prouve pas que le demi-cercle est la courbe championne dans le demi-plan, ni que le cercle est la championne du plan ! Ce que l'on a démontré, c'est seulement que si il existe une courbe championne, alors c'est le demi-cercle dans le demi-plan, ou le cercle dans le plan. L'existence de la courbe championne, en dépit du fait que le seul candidat possible a été identifié, relève de mathématiques plus élaborées. Ce n'est que plusieurs dizaines d'années après Steiner que Karl Weierstrass obtint, en 1879, la première preuve complète que le cercle est effectivement la courbe optimale.
Problème isopérimétrique polygonal
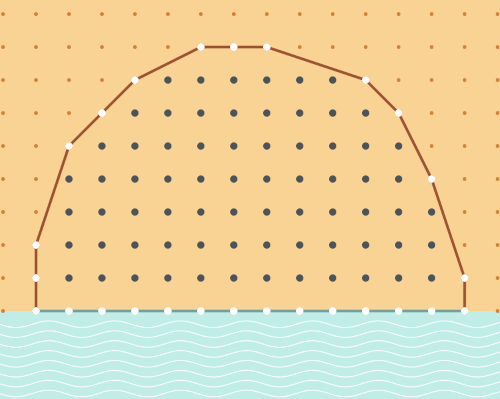
Dans notre animation sur le problème de Didon, c'est une version légèrement différente du problème isopérimétrique qui est proposée : en effet il n'est pas possible d'y tracer un cercle ou un demi-cercle, les seules courbes admises sont des polygones dont les sommets sont des points à coordonnées entières. Toutefois, on peut constater sur cette animation que plus le polygone est proche du cercle (ou du demi-cercle) solution du problème isopérimétrique, plus l'aire délimitée par ce polygone est grande. Dans ce cas précis d'un polygone dont les sommets sont à coordonnées entières, l'avantage est de pouvoir calculer l'aire facilement à l'aide du théorème de Pick : selon ce théorème, l'aire délimitée par une courbe polygonale dont les sommets sont à coordonnées entières vaut $$ A = I + B/2 -1, $$ où $I$ est le nombre de points à coordonnées entières à l'intérieur, et $B$ le nombre de points à coordonnées entières sur le contour du polygone.
Aller à l'animation sur le problème de Didon.
Voir aussi notre poster sur les problèmes isopérimétriques.