On rappelle pour mémoire que la suite des nombres de Fibonacci commence par 1, 1, 2, 3, 5, 8, 13, 21, et se poursuit indéfiniment en calculant à chaque fois le prochain terme comme la somme des deux précédents. Pour tout entier $n\geq1$ on note $F_n$ le $n$-ième nombre de la suite de Fibonacci, de sorte que
$F_1=1$, $F_2=1$, $F_3=2$, $F_4=3\ldots$.
Les propriétés classiques de cette suite sont utilisées dans le tour de passe-passe géométrique décrit ci-dessous, qui peut être vu comme une variante d'un puzzle du célèbre Lewis Caroll.
Triangles de Fibonacci
On appelle ici triangle de Fibonacci un triangle rectangle dont les côtés de l'angle droit ont pour mesures deux nombres de Fibonacci consécutifs.
La figure ci-dessous montre des exemples de tels triangles.
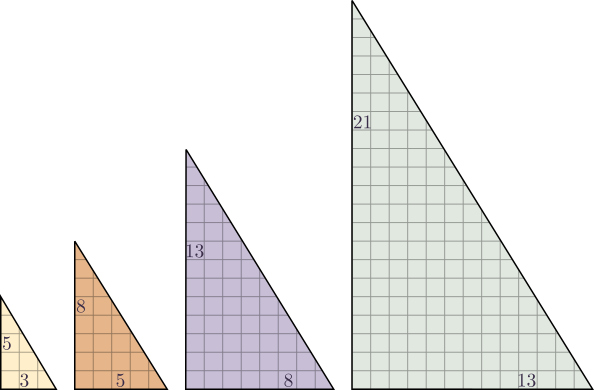
Par construction de la suite de Fibonacci, les mesures indiquées sur le troisième triangle sont égales à la somme des mesures correspondantes sur les deux premiers :
$$ 8=3+5 $$
et
$$ 13=5+8. $$
On peut donc placer les deux premiers triangles par-dessus le troisième pour obtenir la figure suivante :
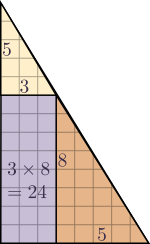
Configuration 1
On peut également échanger les positions des deux plus petits triangles pour obtenir une nouvelle configuration :
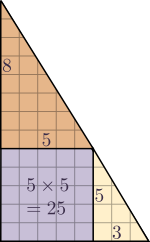
Configuration 2
Dans la première configuration, les deux plus petits triangles laissent apparaître un morceau du troisième de forme rectangulaire et de dimensions $3\times 8$, donc d'aire 24. Dans la seconde, le morceau apparent du grand triangle est un carré de côté 5, donc d'aire 25...
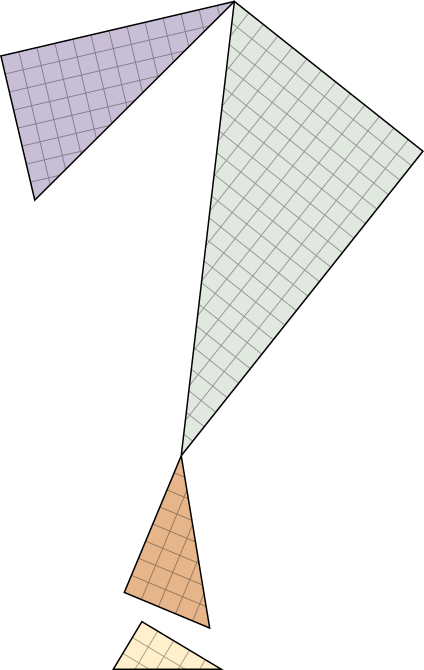
Le phénomène se reproduit quasiment à l'identique avec des triangles de Fibonacci plus grands. Par exemple, avec le quatrième triangle de Fibonacci dessiné au début et les deux précédents, on obtient les deux configurations suivantes :
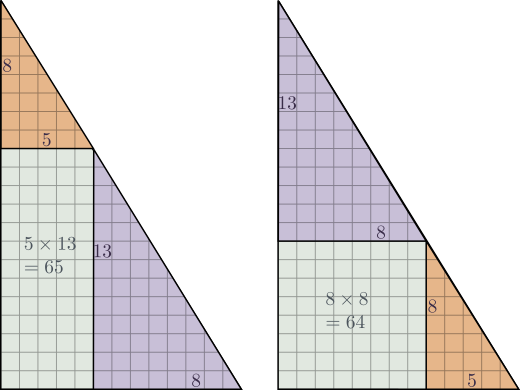
À gauche, le rectangle resté apparent mesure $5\times 13$, il est donc d'aire 65, tandis qu'à droite le carré resté apparent est de côté 8, donc d'aire 64...
Comment expliquer cette mystérieuse variation des aires ?
Trigonométrie et quotients de nombres de Fibonacci consécutifs
Le voile sur le mystère des aires qui varient est rapidement levé si on s'intéresse de plus près aux angles des triangles de Fibonacci.
Nous avons représenté sur la figure suivante les angles au sommet du petit côté dans les quatre triangles de Fibonacci considérés ci-dessus.
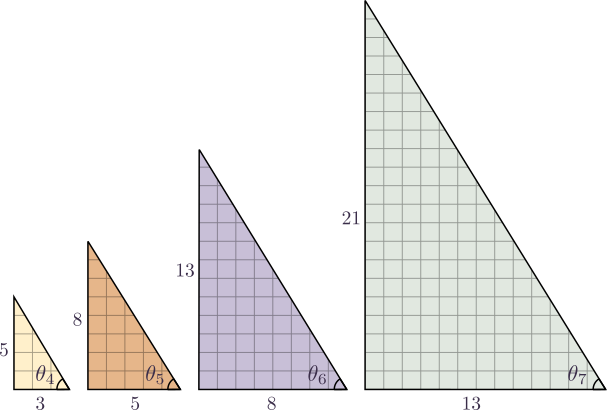
L'application des formules de trigonométrie usuelles dans le triangle rectangle donne, dans le triangle de gauche :
$$ \tan\theta_4=\dfrac{5}{3}\simeq 1,667. $$
Dans le second triangle, on obtient
$$ \tan\theta_5=\dfrac{8}{5}= 1,6. $$
Dans le troisième triangle, on a
$$ \tan\theta_6=\dfrac{13}{8}= 1,625. $$
Enfin, dans le triangle de droite :
$$ \tan\theta_7=\dfrac{21}{13}\simeq 1,615. $$
Bien que très proches les unes des autres, les tangentes de ces angles ne sont pas égales, ainsi les angles eux-mêmes ne sont pas de même mesure. Contrairement à l'impression que l'on a en observant rapidement ces figures, les triangles de Fibonacci ne sont donc pas tous semblables les uns aux autres. En conséquence, dans les configurations où l'on a superposé deux triangles de Fibonacci plus petits sur un troisième plus grand, le sommet commun aux deux petits triangles n'est pas exactement placé sur l'hypoténuse du plus grand. Cela ne se voit pas sur les dessins présentés car l'épaisseur des traits est trop importante. Mais si on agrandit le détail des figures, en amincissant les traits représentants les côtés, on obtient ceci :
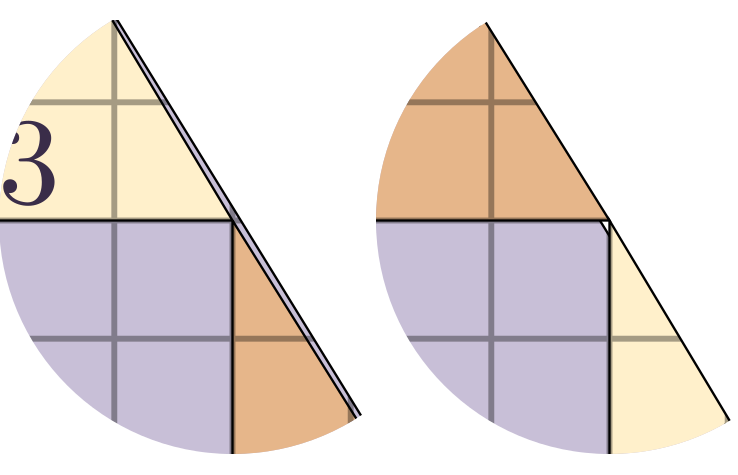
Détails des configurations 1 (à gauche) et 2 (à droite)
Dans la première configuration, l'aire du grand triangle est légèrement supérieure à la somme des aires des petits triangles et de celle du rectangle. Dans la seconde, l'aire du grand triangle est cette fois légèrement inférieure à la somme des aires des petits triangles et de celle du carré.
En général pour un entier $n\geq1$, dans le triangle de Fibonacci dont les côtés de l'angle droit ont pour mesures respectives le $n$-ième nombre de Fibonacci $F_n$ et le suivant $F_{n+1}$, la tangente de l'angle $\theta_n$ au sommet du petit côté vaut
$$ \tan \theta_n = \dfrac{F_{n+1}}{F_n}. $$
Or, selon une propriété classique de la suite des nombres de Fibonacci, ce quotient $\frac{F_{n+1}}{F_n}$ se rapproche de plus en plus du nombre d'or
$$ \varphi = \dfrac{1+\sqrt{5}}{2}\simeq 1,618034. $$
Ainsi plus $n$ devient grand et plus l'angle au sommet du petit côté se rapproche d'une valeur fixe : l'angle limite est celui dont la tangente vaut le nombre d'or. En fait, l'angle au sommet du petit côté dans le triangle de Fibonacci est alternativement au-dessus et en-dessous de cette valeur, en s'en rapprochant de plus en plus. Et cette convergence est si rapide que même pour des valeurs de $n$ assez petites, la différence des mesures des angles ne se distingue pas à l'œil nu.
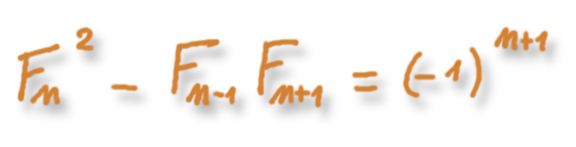
La formule de Cassini
Ce tour de passe-passe illustre également une autre propriété classique de la suite des nombres de Fibonacci : on constate dans les deux exemples présentés ci-dessus que l'aire du carré obtenu dans une configuration diffère d'une unité de celle du rectangle obtenu dans l'autre configuration.
Cette propriété est générale, et porte le nom de formule de Cassini : la différence entre le carré d'un nombre de Fibonacci et le produit de celui qui le précède avec celui qui le suit vaut $\pm1$ alternativement. On calcule facilement cette différence pour les premières valeurs de $n$ :
$$ (F_2)^2-F_1F_3 = 1^2-1\times2=-1, $$
$$ (F_3)^2-F_2F_4 = 2^2-1\times3= 1, $$
$$ (F_4)^2-F_3F_5 = 3^2-2\times5= -1, $$
$$ (F_5)^2-F_4F_6 = 5^2-3\times8= 1. $$
En général, la formule de Cassini affirme que pout tout entier $n\geq2$,
$$ (F_n)^2-F_{n-1}F_{n+1}=(-1)^{n+1}. $$
Cette formule est très simple à démontrer par récurrence. On peut pour cela s'aider de dessins construits dans un rectangle de dimensions $F_n\times F_{n+1}$ (ici $n$ est un entier arbitraire, $n\ge3$).
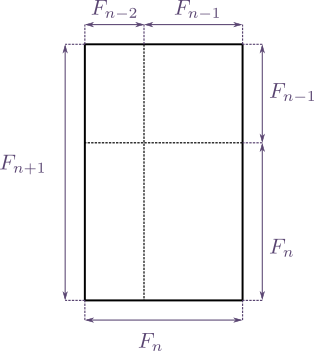 Pour découper le rectangle ci-dessus, on a simplement utilisé le fait que chaque nombre de Fibonacci est la somme des deux qui le précèdent dans la suite. À partir de ce découpage on trouve une interprétation géométrique de la quantité concernée par la formule de Cassini, à savoir la différence
$$d_n:=(F_n)^2-F_{n-1}F_{n+1}.$$
Pour découper le rectangle ci-dessus, on a simplement utilisé le fait que chaque nombre de Fibonacci est la somme des deux qui le précèdent dans la suite. À partir de ce découpage on trouve une interprétation géométrique de la quantité concernée par la formule de Cassini, à savoir la différence
$$d_n:=(F_n)^2-F_{n-1}F_{n+1}.$$
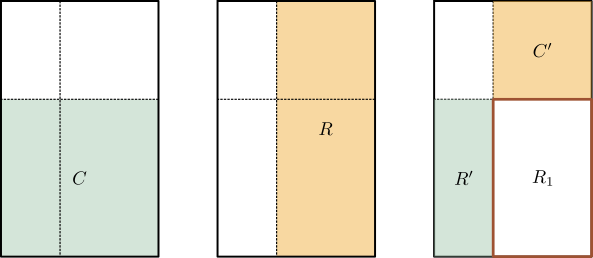 Le carré $C$ étant de côté $F_n$, le terme $(F_n)^2$ peut être vu comme l'aire de ce carré. De même, le terme $F_{n-1}F_{n+1}$ est l'aire du rectangle $R$. On a donc
$$ d_n=\text{aire}(C)-\text{aire}(R).$$
Mais puisque le carré $C$ et le rectangle $R$ ont pour intersection le rectangle $R_1$, on a aussi
$$ d_n=\text{aire}(R')-\text{aire}(C').$$
Or, le rectangle $R'$ est de dimensions $F_n\times F_{n-2}$, et $C'$ est un carré de côté $F_{n-1}$. On obtient alors
$$ d_n = F_n F_{n-2} - (F_{n-1})^2 = -d_{n-1}. $$
Comme on l'a déjà constaté, $d_2=-1$. Par une récurrence immédiate, ceci prouve que la formule de Cassini est vraie pour tout $n\ge2$.
Le carré $C$ étant de côté $F_n$, le terme $(F_n)^2$ peut être vu comme l'aire de ce carré. De même, le terme $F_{n-1}F_{n+1}$ est l'aire du rectangle $R$. On a donc
$$ d_n=\text{aire}(C)-\text{aire}(R).$$
Mais puisque le carré $C$ et le rectangle $R$ ont pour intersection le rectangle $R_1$, on a aussi
$$ d_n=\text{aire}(R')-\text{aire}(C').$$
Or, le rectangle $R'$ est de dimensions $F_n\times F_{n-2}$, et $C'$ est un carré de côté $F_{n-1}$. On obtient alors
$$ d_n = F_n F_{n-2} - (F_{n-1})^2 = -d_{n-1}. $$
Comme on l'a déjà constaté, $d_2=-1$. Par une récurrence immédiate, ceci prouve que la formule de Cassini est vraie pour tout $n\ge2$.
Voir d'autres activités sur la suite de Fibonacci.







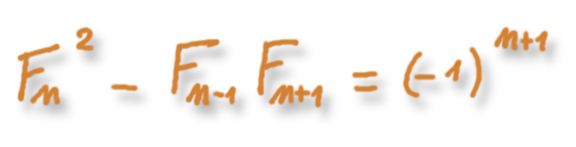
 Pour découper le rectangle ci-dessus, on a simplement utilisé le fait que chaque nombre de Fibonacci est la somme des deux qui le précèdent dans la suite. À partir de ce découpage on trouve une interprétation géométrique de la quantité concernée par la formule de Cassini, à savoir la différence
$$d_n:=(F_n)^2-F_{n-1}F_{n+1}.$$
Pour découper le rectangle ci-dessus, on a simplement utilisé le fait que chaque nombre de Fibonacci est la somme des deux qui le précèdent dans la suite. À partir de ce découpage on trouve une interprétation géométrique de la quantité concernée par la formule de Cassini, à savoir la différence
$$d_n:=(F_n)^2-F_{n-1}F_{n+1}.$$
 Le carré $C$ étant de côté $F_n$, le terme $(F_n)^2$ peut être vu comme l'aire de ce carré. De même, le terme $F_{n-1}F_{n+1}$ est l'aire du rectangle $R$. On a donc
$$ d_n=\text{aire}(C)-\text{aire}(R).$$
Mais puisque le carré $C$ et le rectangle $R$ ont pour intersection le rectangle $R_1$, on a aussi
$$ d_n=\text{aire}(R')-\text{aire}(C').$$
Or, le rectangle $R'$ est de dimensions $F_n\times F_{n-2}$, et $C'$ est un carré de côté $F_{n-1}$. On obtient alors
$$ d_n = F_n F_{n-2} - (F_{n-1})^2 = -d_{n-1}. $$
Comme on l'a déjà constaté, $d_2=-1$. Par une récurrence immédiate, ceci prouve que la formule de Cassini est vraie pour tout $n\ge2$.
Le carré $C$ étant de côté $F_n$, le terme $(F_n)^2$ peut être vu comme l'aire de ce carré. De même, le terme $F_{n-1}F_{n+1}$ est l'aire du rectangle $R$. On a donc
$$ d_n=\text{aire}(C)-\text{aire}(R).$$
Mais puisque le carré $C$ et le rectangle $R$ ont pour intersection le rectangle $R_1$, on a aussi
$$ d_n=\text{aire}(R')-\text{aire}(C').$$
Or, le rectangle $R'$ est de dimensions $F_n\times F_{n-2}$, et $C'$ est un carré de côté $F_{n-1}$. On obtient alors
$$ d_n = F_n F_{n-2} - (F_{n-1})^2 = -d_{n-1}. $$
Comme on l'a déjà constaté, $d_2=-1$. Par une récurrence immédiate, ceci prouve que la formule de Cassini est vraie pour tout $n\ge2$.