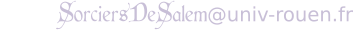Le décompte des spirales sur les pommes de pin ou les fleurs de la famille des tournesols donne très souvent deux nombres de Fibonacci successifs. (Si vous n'avez pas sous la main le matériel végétal pour le vérifier, nous vous invitons à compter sur cette page.)
Il semble difficile de croire à une simple coïncidence : la régularité de ce phénomène semble plutôt révéler la mise en œuvre de principes mathématiques dans les mécanismes complexes de la croissance des plantes.
Ce sont des travaux de phyllotaxie, la science qui étudie les arrangements (géométriques) des feuilles, fleurs ou pétales des plantes, qui ont mis en évidence ces principes dès le XIXe siècle (voir notamment l'Essai sur la disposition des feuilles curvisériées de Louis et Auguste Bravais, Annales des sciences naturelles, tome 7, 1837, 42—110). Les mathématiciens et informaticiens se sont ensuite penchés sur la question, et ont travaillé sur des modélisations permettant de décrire de manière simplifiée les mécanismes de formation des végétaux.
L'objectif de cette page est de fournir quelques explications mathématiques à la présence des nombres de Fibonacci dans ce contexte botanique, et d'établir le lien avec les remarquables propriétés du nombre d'or. Pour cela nous nous appuyons sur un modèle de formation des fleurs de tournesol, que vous pouvez expérimenter en jouant avec cette application.
Un modèle de formation des fleurs de tournesol
Ce que l'on nomme usuellement une «fleur» de tournesol (ou d'une plante de la même famille comme la marguerite ou l'aster) est en fait un réceptacle floral, le capitule, portant de nombreuses petites fleurs appelées fleurons. C'est la disposition de ces fleurons (puis des graines qu'ils donneront ensuite) qui révèle les fameuses spirales. Le modèle de formation de ces spirales que nous utilisons est inspiré des travaux de Helmut Vogel (A better way to construct the sunflower head, Mathematical Biosciences 44, 1979). Il repose sur un principe général : les organes d'une plante comme les feuilles, les pétales, ou ici les fleurons, poussent les uns à la suite des autres en formant à chaque fois un angle fixé avec le précédent. Cet angle s'appelle l'angle de divergence, et on l'exprime en général comme une proportion d'un tour complet. Ainsi, un angle de divergence qui vaut 1/6 signifie que l'on tourne d'un sixième de tour autour du centre du capitule pour placer le fleuron suivant.
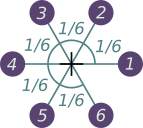
Dans le modèle que nous proposons, si la position du nouveau fleuron après cette rotation vient à se superposer avec un fleuron déjà existant, on augmente la distance au centre du capitule de façon à s'écarter suffisamment de l'ancien fleuron. De cette façon les fleurons successifs sont à une distance de plus en plus grande du centre du capitule.
Dans la réalité, c'est plutôt la situation inverse qui se passe : les fleurons se forment près du centre puis s'en éloignent radialement, laissant de la place pour les nouveaux (voir plus d'explications sur cette page), mais cette simplification ne change pas l'allure générale de la figure obtenue à la fin du processus. Dans le modèle, le processus se termine lorsque l'on arrive au bord d'un disque dont la taille est fixée à l'avance.
Des branches dans les fleurs
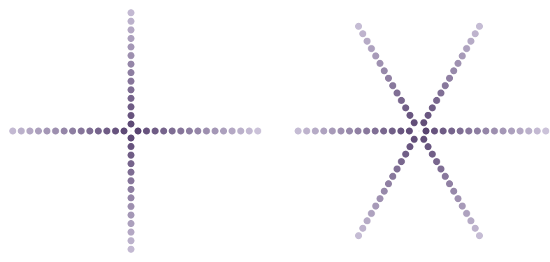
Mais quelle est la figure obtenue à ce moment là ? L'allure de celle-ci dépend fortement de la valeur de l'angle de divergence. Considérons d'abord le cas où cette valeur est une fraction simple : par exemple, si l'on effectue des rotations d'angle $1/4$ ou $1/6$, on obtient sans grande surprise les résultats ci-dessous :
Un angle de divergence intéressant est donné par une autre fraction : la figure suivante montre la disposition obtenue lorsque cet angle est fixé à $11/23$. (Cet exemple, comme une bonne partie de l'exposé présenté ici, est inspiré de cette excellente vidéo en anglais, proposée par Numberphile.)

Du point de vue de la plante, les angles de divergence proposés ci-dessus ne sont pas vraiment intéressants, car une bonne partie de la place disponible sur le capitule n'est pas exploitée. La raison ici est simple : dans le cas $1/4$ par exemple, après avoir appliqué 4 étapes du processus de construction, on a effectué un tour complet donc la direction dans laquelle pousse le nouveau fleuron est exactement la même que celle utilisée 4 fleurons auparavant. On obtient finalement une figure à 4 branches qui n'utilise que 4 directions. De même pour $1/6$ on obtient 6 branches puisqu'après 6 itérations on retourne sur la direction de départ. Dans le cas $11/23$, 23 étapes du processus font 11 tours complets, et donc on revient dans la même direction tous les 23 fleurons. La figure présente donc 23 branches à l'extérieur (ce qui se passe vers le centre est un peu plus subtil, nous reviendrons dessus peu après). De même, ce type de phénomène se manifestera à chaque fois que l'on choisit un angle de divergence rationnel, c'est-à-dire qui s'écrit comme le quotient de deux nombres entiers. Il est donc tentant de tester ce qui se passe lorsque l'angle de divergence n'est pas rationnel.
Un premier exemple de nombre irrationnel qui vient à l'esprit est celui du fameux nombre $\pi$, qui intervient dans le calcul du périmètre du cercle et dans tant d'autres formules mathématiques (voir cette page pour découvrir quelques activités amusantes autour de $\pi$). Voyons donc ce qui se passe si l'on choisit un angle de divergence égal à $1/\pi$.
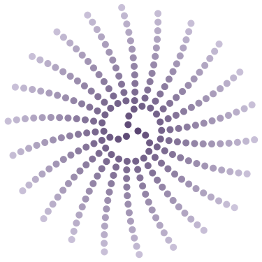
Le nombre $\pi$ est trop rationnel !
Curieusement, alors que $\pi$ (donc aussi $1/\pi$) n'est pas un nombre rationnel, la figure est du même type que celle obtenue pour un rationnel comme $11/23$, avec ici 22 branches à l'extérieur. Une petite différence néanmoins est que ces branches sont légèrement courbes.
L'examen attentif de la figure donnée pour $1/\pi$ va nous permettre de mieux comprendre les qualités attendues de l'angle de divergence pour la plante. Commençons par bien regarder ce qui se passe vers le centre : le processus de formation commence par dessiner 3 branches courbées. On peut expliquer facilement la présence de ces 3 branches : l'écriture décimale de $\pi$ commence par $3,14159\ldots$, donc dans une première approximation, $\pi$ est proche de 3. Le nombre $1/\pi$ est donc proche de $1/3$. Or un angle de divergence $1/3$ donnera une figure à 3 branches rectilignes, et ce qui se passe vers le centre est donc une approximation de ces 3 branches. Les 3 branches sont ici courbées car $1/\pi$ est en fait légèrement inférieur à $1/3$. Puis, à mesure que le rayon pour former les nouveaux fleurons augmente, approcher l'angle de divergence par $1/3$ devient beaucoup trop grossier. C'est pourquoi les 3 branches centrales finissent par disparaître. Ce phénomène est également observé vers le centre de la figure pour $11/23$ : dans une première approximation, $11/23$ est proche de 1/2 et donc on observe un comportement similaire à ce qui se passerait avec un angle de divergence égal à $1/2$ : une figure à 2 branches opposées.
Comment expliquer ensuite la formation de 22 nouvelles branches dans la figure ? Il faut savoir qu'une autre approximation simple du nombre $\pi$, beaucoup plus précise que $3$, est donnée par la fraction $22/7\simeq 3,142857$. Ainsi une très bonne approximation de l'angle de divergence devient $7/22$. Or on sait que pour un angle de divergence égal à $7/22$ on observerait une figure à 22 branches rectilignes. Comme l'approximation de $1/\pi$ par $7/22$ est très bonne mais pas exacte, on obtient ces 22 branches légèrement courbes.
En dépit du fait que $1/\pi$ n'est pas un nombre rationnel, on voit que cette valeur n'est pas non plus un bon choix d'angle de divergence pour la plante, car trop d'espace est perdu sur le capitule ! Et on en comprend la raison : le nombre $1/\pi$, bien qu'irrationnel, est trop bien approché par des nombres rationnels. Pour que les fleurons soient disposés de manière très efficace sur le capitule, il faudrait donc utiliser un angle de divergence qui soit le plus mal possible approché par des nombres rationnels.
Initiation aux fractions continues
La théorie de l'approximation d'un nombre réel quelconque par un nombre rationnel, que l'on appelle aussi approximation diophantienne est donc centrale dans ce problème. Un outil essentiel pour traiter de cette question est la représentation des nombres sous forme de fraction continue : étant donné un nombre $\alpha>0$, il est toujours possible de le représenter par une expression de la forme $$ \alpha=a_0 + \cfrac{1}{a_1+\cfrac{1}{a_2+\cfrac{1}{a_3+\cdots}}} $$ où $a_0,a_1,a_2\ldots$ sont des nombres entiers positifs appelés les quotients partiels du nombre $\alpha$. Tous ces quotients partiels sont supérieurs ou égaux à 1, sauf éventuellement $a_0$ qui est nul dans le cas où $0<\alpha<1$. Si $\alpha$ est un nombre rationnel, la suite de ses quotients partiels est finie. Par exemple, pour $\alpha=11/23$, sa représentation en fraction continue est $$ \dfrac{11}{23} = \cfrac{1}{2+\cfrac{1}{11}}. $$ En revanche, un nombre irrationnel $\alpha$ donne une suite infinie de quotients partiels. Par exemple, le développement en fraction continue du nombre $1/\pi$ s'écrit $$ 1/\pi = \cfrac{1}{3 + \cfrac{1}{7+\cfrac{1}{15+\cfrac{1}{1+\cdots}}}} $$ et ne s'arrête jamais.
On peut alors construire des nombres rationnels qui approchent bien un nombre irrationnel $\alpha$ en tronquant cette suite et en calculant le nombre rationnel qui correspond à ces premiers quotients partiels. On obtient ce que l'on appelle une réduite de $\alpha$. Par exemple, les premières réduites du nombre $1/\pi$ sont $$\cfrac{1}{3}$$ et $$ \cfrac{1}{3+\cfrac{1}{7}}=\cfrac{7}{22}. $$ Un des résultats remarquables de cette théorie est que les réduites ainsi construites fournissent les meilleures approximations possibles du nombre $\alpha$ par des nombres rationnels (en un sens précis, que nous ne détaillons pas ici). Et l'approximation fournie est d'autant meilleure que le premier quotient partiel négligé est grand. Ainsi la réduite $7/22$ fournit une très bonne approximation de $1/\pi$ car le premier quotient partiel négligé vaut ici 15, qui est déjà un grand entier comparé à 1. C'est pourquoi les 22 branches se voient si nettement dans la figure de l'angle de divergence $1/\pi$.
Le nombre d'or s'impose
Nous avons maintenant tous les éléments pour déterminer quel est le meilleur choix pour l'angle de divergence : il nous faut une valeur $\alpha$ qui soit le moins bien approchée possible par des nombres rationnels, donc le moins bien approchée possible par ses réduites. Or cela sera le cas quand les quotients partiels seront les plus petits possible. Mais la plus petite valeur possible pour un quotient partiel est 1, donc le choix le plus pertinent pour l'angle de divergence, si on le prend entre 0 et 1, est $$ \alpha = \cfrac{1}{1 + \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}}}. $$ Combien vaut ce nombre ? La forme de ce développement montre qu'il vérifie l'égalité $$ \alpha = \cfrac{1}{1 + \alpha}, $$ donc qu'il est solution de l'équation $$ \alpha^2+\alpha-1=0. $$ La solution positive de l'équation ci-dessus est $$ \alpha = \cfrac{\sqrt{5}-1}{2}=1/\varphi, $$ où $\varphi= \cfrac{\sqrt{5}+1}{2}$ est le célèbre nombre d'or ! Ainsi les fractions continues nous amènent au choix optimum de l'angle de divergence, celui qui est le plus mal approché par des nombres rationnels : c'est l'angle dont le rapport avec un tour complet vaut l'inverse du nombre d'or, et que l'on nomme l'angle d'or. Voyons la figure donnée par le modèle ci-dessus dans ce cas.

On observe effectivement dans le cas de l'angle d'or une bien meilleure utilisation de l'espace disponible : les fleurons sont disposés régulièrement sans laisser d'espace vide important sur le capitule. On note également une réelle ressemblance avec la disposition observée sur de vrais tournesols : l'évolution naturelle a conduit ces plantes à adopter l'angle d'or comme angle de divergence !
Le retour de Fibonacci
Arrivés à cette première conclusion, et sachant que le nombre d'or est indissociable de la suite de Fibonacci, on peut commencer à deviner un fort lien entre la présence des nombres de Fibonacci dans les spirales des tournesols et le choix de cet angle d'or comme angle de divergence. En fait, ces spirales correspondent aux «branches» que l'on observe dans les cas d'un angle de divergence (presque) rationnel : chaque réseau de spirales est associé à une approximation rationnelle de l'angle d'or par l'une de ses réduites. Comme dans les cas $1/6$, $11/23$ ou $1/\pi$ vus précédemment, le nombre de spirales (ou de branches) est donné par le dénominateur de la fraction définie par la réduite. Or ces réduites ont pour dénominateurs successifs... les nombres de Fibonacci ! Elles sont en fait les quotients de nombres de Fibonacci successifs : la première réduite est $1/1$, et les suivantes sont $$ \cfrac{1}{1 + \cfrac{1}{1}} = \cfrac{1}{2} ; $$ $$ \cfrac{1}{1+\cfrac{1}{1 + \cfrac{1}{1}}} = \cfrac{2}{3} ;$$ $$ \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1 + \cfrac{1}{1}}}} = \cfrac{3}{5} \cdots $$
L'image ci-dessous montre un capitule de tournesol idéal et assez grand, sur lequel on peut visualiser les réseaux de spirales correspondant à différentes réduites du nombre d'or (il suffit de les activer à l'aide des boutons situés sous l'image). On peut ainsi se rendre compte que les réseaux associés à deux réduites consécutives tournent dans des sens opposés, et se chevauchent sur des zones d'autant plus éloignées du centre que les dénominateurs des réduites sont des grands nombres de Fibonacci. Ces dénominateurs sont précisément les nombres de spirales dans chacun des réseaux. C'est la raison pour laquelle on observe dans la nature deux nombres de Fibonacci consécutifs, mais qui ne sont pas toujours les mêmes : ils dépendent de la taille du capitule considéré.







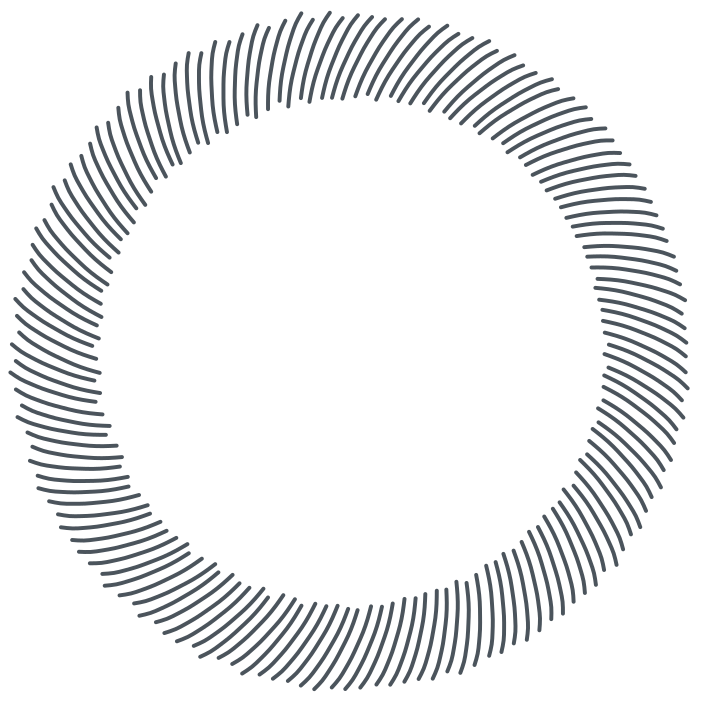
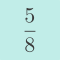
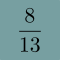


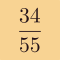


La rotation de l'angle d'or possède une autre propriété en lien avec la suite de Fibonacci, qui est également une conséquence de la nature des réduites du nombre d'or. Prenons un objet dans le plan (pour fixer les idées, disons un pétale) et répétons sur cet objet la rotation de l'angle d'or, tant que la nouvelle position du pétale ne chevauche pas celle de départ. Le nombre maximum de pétales obtenus sans chevauchement est toujours un nombre de Fibonacci, qui dépend du rapport entre la taille du pétale et son éloignement au centre de la rotation.
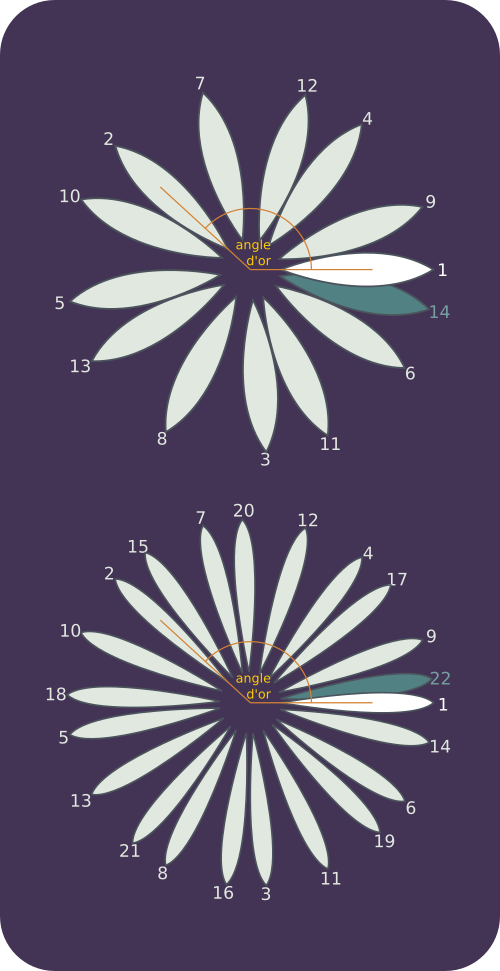
Quelques commentaires sur la figure ci-dessus : l'«angle d'or» dessiné en jaune mesure approximativement $137,5°$. Il fait moins qu'un demi-tour, ce qui semble contradictoire avec la valeur numérique de $1/\varphi\simeq 0,618$. Mais tourner de $1/\varphi$ dans un sens revient à tourner de $1-1/\varphi$ dans l'autre sens, or $(1-1/\varphi)\times 360\simeq 137,5$. Par ailleurs, les pétales sont numérotés dans l'ordre de leur formation à mesure que l'on a itéré la rotation : remarquez que deux pétales côte à côte ont toujours des numéros dont la différence est un nombre de Fibonacci !