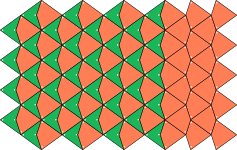
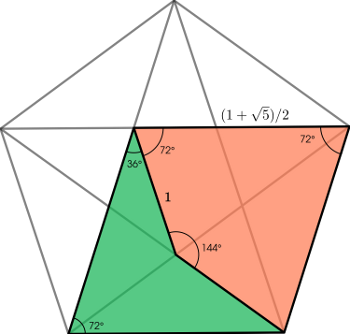
Le physicien et mathématicien Roger Penrose a découvert dans les années 1970 des pavages du plan, constitués de deux types seulement de carreaux, assemblés de manière non périodique (on ne peut pas obtenir ces pavages par la répétition d'un seul et même motif). L'un des pavages découverts par Penrose utilise les deux pièces dessinées ci-dessous à l'intérieur d'un pentagone régulier, appelées « fléchette » (en vert) et « cerf-volant » (en orange)

Quelques activités autour des pavages de Penrose
Puzzles
Commencez par télécharger l'image ci-dessous, imprimez-la puis découpez les fléchettes et les cerfs-volants.
Pavages périodiques. Réalisez un carrelage assez grand pour cacher un quart de feuille A4, en n'utilisant que des cerfs-volants, sans qu'ils se recouvrent ni qu'il y ait de trous. Faites de même en n'utilisant que des fléchettes.
Pavages quasi-périodiques. Réalisez un carrelage assez grand pour cacher un quart de feuille A4, en utilisant cerfs-volants et fléchettes, et en respectant la règle des gommettes ci-dessous.
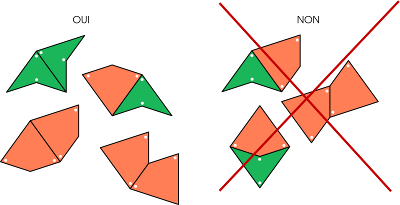
Étendez votre pavage tant que possible.
Coloriages
téléchargez le pavage de Penrose à colorier ci-dessous, et imprimez-le.
Comptez les étoiles Dans l'univers de Penrose, on trouve beaucoup d'objets intéressants, comme ceux représentés ci-dessous. Amusez-vous à les colorier et à les compter.

On peut aussi trouver des animaux (poissons, tortues, papillons, renards...). Laissez aller votre imagination ! Nous avons même trouvé une voiture...

Fléchettes et cerfs-volants tricolores. Comme toutes les cartes planes, les pavages de Penrose peuvent se colorier en 4 couleurs de sorte que deux régions avec un bord commun soient de couleurs différentes. En 2002, William Paulsen a prouvé qu'en fait il suffit de 3 couleurs pour colorier les pavages de Penrose de type fléchettes et cerfs-volants. Pourriez-vous montrer qu'il n'est pas possible de le faire avec 2 couleurs ? Sauriez-vous trouver un coloriage du pavage avec 3 couleurs ?
Quelques liens
- Une magnifique animation sur les pavages de Penrose ;
- Un poster sur les pavages de Penrose ;
- Comment nous avons réalisé les pavages de Penrose avec Inkscape et les systèmes de Lindenmayer : voir ici.