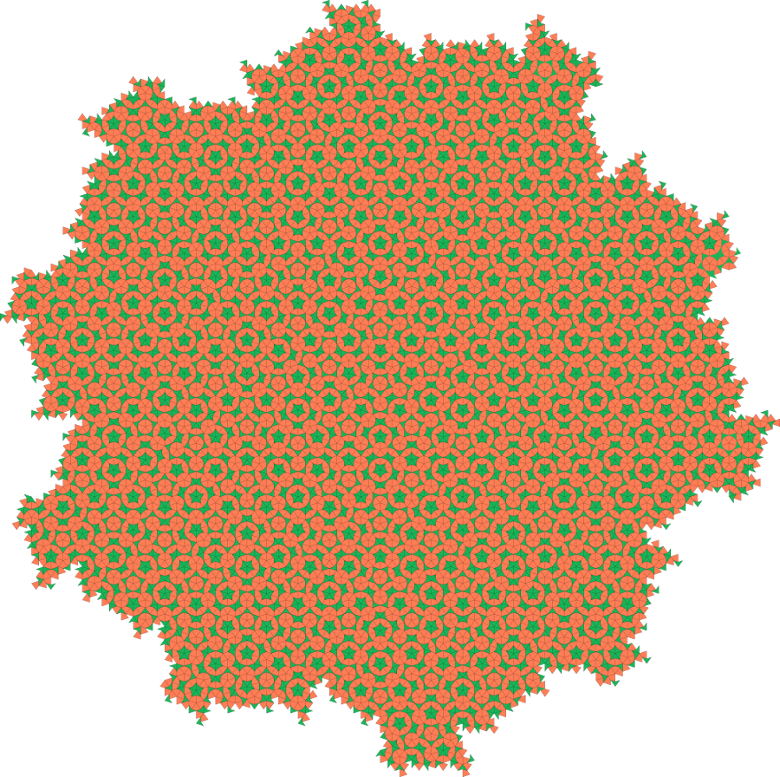
Le but de cette page est d'expliquer comment nous avons réalisé des pavages de Penrose de type « fléchettes et cerfs-volants » en utilisant le logiciel de dessin vectoriel Inkscape et les L-systèmes (ou systèmes de Lindenmayer).
Quelques mots sur les L-systèmes
Un L-système est un procédé algorithmique, inventé en 1968 par le biologiste hongrois Aristid Lindenmayer pour modéliser le processus de développement de plantes. Il consiste en un ensemble de symboles (qui modélisent les cellules de la plante) et de règles de réécriture (qui modélisent la façon dont les cellules se divisent, donc sont remplacées par un ensemble plus complexe de cellules).
Le point de départ est une suite finie de symboles appelée axiome. Puis, chaque étape consiste à remplacer chacun des symboles de la suite courante par un ou plusieurs symboles donnés par les règles de réécriture.
Les L-systèmes avec Inkscape
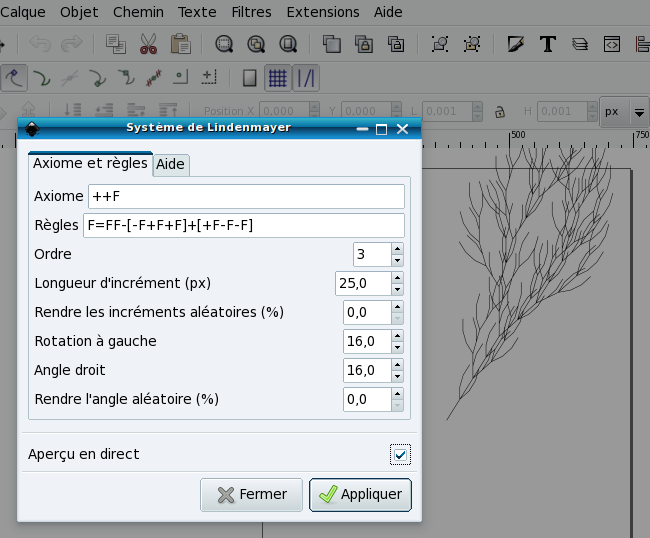
Inkscape propose une extension implémentant des L-systèmes accessible via le menu Extension > Rendu > Système de Lindenmayer Dans cette implémentation, certains symboles sont interprétés de façon particulière par Inkscape : les lettres de A à F tracent un segment de longueur une unité dans la direction courante, tandis que les lettres G à L déplacent la position courante d'une unité sans tracer. Les symboles + et - tournent respectivement la direction de tracé d'un angle prédéfini dans le sens des aiguilles d'une montre ou dans le sens inverse. Les crochets [] permettent de revenir au point courant après avoir effectué une partie du tracé. Le symbole | indique un demi-tour.
Au lancer de l'extension, une fenêtre invite l'utilisateur à définir ces différents paramètres, l'axiome, les règles de substitution et le nombre d'étapes à effectuer.
Adaptation aux pavages de Penrose
Les L-systèmes sont parfaitement adaptés à la génération des pavages de Penrose car ceux-ci sont précisément obtenus par itération de substitutions : à chaque étape, un cerf-volant est remplacé par deux cerfs-volants et une fléchette, et chaque fléchette est remplacée par un cerf-volant et une fléchette.
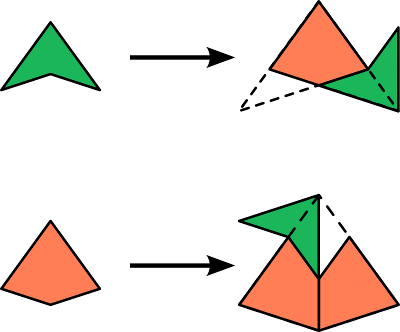
Néanmoins, l'implémentation d'Inkscape ne permet pas de les réaliser directement car elle n'autorise le tracé que de segments qui mesurent tous la même longueur. Or les figures à dessiner pour les pavages de Penrose comportent des côtés qui sont de deux longueurs différentes, le rapport des deux longueurs étant égal au nombre d'or.
Nous avons donc légèrement modifié l'extension « systèmes de Lindenmayer » d'Inkscape, afin d'ajouter un paramètre supplémentaire appelé facteur. Dans cette nouvelle version, Inkscape interprètes les lettres de la façon suivante : A, B et C tracent un segment de longueur 1 tandis que D, E et F tracent un segment de longueur 1×facteur. De même, G, H et I effectuent un déplacement de longueur 1 unité, tandis que J, K et L déplacent d'une longueur 1×facteur.
Vous pouvez télécharger les fichiers nécessaires pour faire fonctionner cette extension : penrose.inx et penrose.py. Ces fichiers sont à copier (sous linux !) dans le sous-répertoire de votre répertoire personnel : ~/.config/inkscape/extensions/
Il reste à définir les règles et l'axiome de départ. Nous avons choisi le symbole U pour le cerf-volant, et V pour la fléchette. L'angle de rotation est fixé à 36°, et le facteur est une approximation du nombre d'or 1,618034. Le tracé d'un cerf-volant se code par la suite de caractères [+D---A-A---D], et celui d'une fléchette par [+++A----D---D----A].
Lors de la substitution, un cerf-volant est remplacé par deux cerfs-volants et une fléchette : [+G|V][+GJ----U][-GJ++++U], et une fléchette est remplacée par un cerf-volant et une fléchette : [J|U][++G++V].
Il faut supprimer les tracés de l'étape précédente : A=; D=;. Enfin, il faut multiplier à chaque étape les longueurs des sauts par le nombre d'or, sauf à la première ! On commence donc par G qui se transforme en H (même taille) puis H se transforme en K (il est donc multiplié par le nombre d'or), qui sera lui-même multiplié par le nombre d'or en se transformant en HK. De même, à la première étape J se transforme en K qui a la même taille : G=H; J=K; H=K; K=HK;
Récapitulons les règles :
U=[+D---A-A---D][+G|V][+GJ----U][-GJ++++U];
V=[+++A----D---D----A][J|U][++G++V];
A=; D=; G=H; J=K; H=K; K=HK;
On peut commencer avec juste U ou V. Sur l'exemple ci-dessous nous commençons avec un décagone formé par 5 cerfs-volants, ce qui se code par l'axiome [U]++[U]++[U]++[U]++[U].
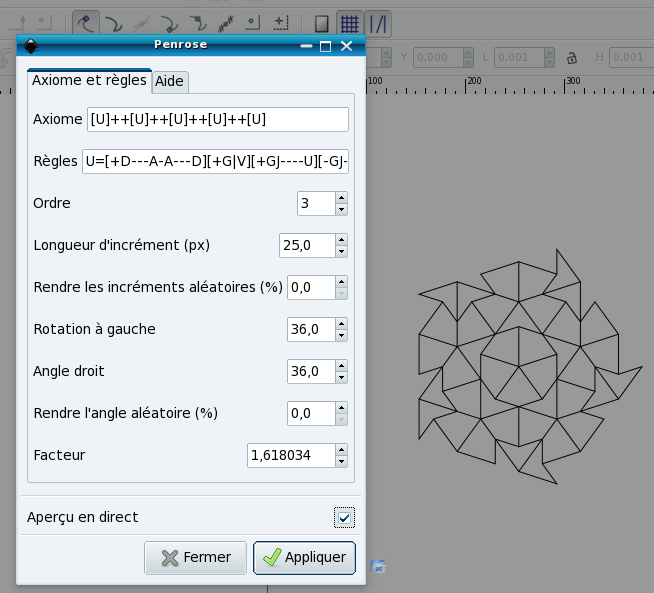
Voici ce qu'on obtient avec 9 étapes, après mise en couleurs :