Notre jeu de taquin basé sur les décimales de $\pi$ est fortement inspiré de celui proposé par Sam Loyd à la fin du XIXe siècle, qui comporte 15 plaques indiquant les nombres entiers de 1 à 15. Les nombres sont rangés dans l'ordre, sauf le 14 et le 15 qui sont échangés. Le défi posé par Sam Loyd consistait à tenter de remettre dans le bon ordre les 15 plaques. Selon son auteur, ce puzzle aurait rendu le monde fou car il était impossible à résoudre !

Le taquin impossible de Sam Loyd, figure extraite de Sam Loyd's Cyclopedia of 5000 Puzzles.
Pourquoi le taquin de Sam Loyd est-il impossible ?
L'explication repose sur la mise en évidence d'un invariant, c'est-à-dire une propriété qui ne change pas quels que soient les mouvements que l'on choisit d'effectuer. Si la configuration de départ possède cette propriété tandis que la configuration visée à l'arrivée ne la vérifie pas, il est clairement impossible de résoudre le problème.
Un moyen de définir un bon invariant pour le jeu de taquin de Sam Loyd est expliqué par Michel Coste dans cet article d'Images des Mathématiques. Résumons les idées principales. On fixe d'abord un chemin particulier qui parcourt l'ensemble des cases du taquin. Ce chemin est dessiné sur la figure ci-dessous :
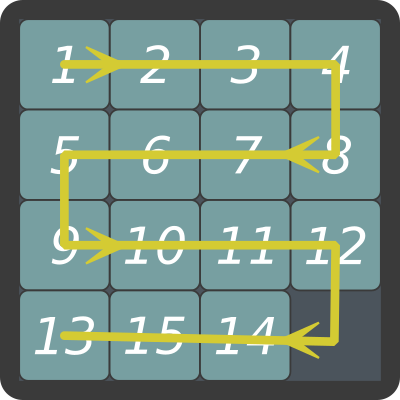
Étant donnée une configuration du taquin, on lui associe la liste des nombres de 1 à 15 dans l'ordre où on les lit le long de ce chemin (on ne tient pas compte de la case vide). Par exemple, la configuration initiale du taquin donne la suite $$ 1\ 2\ 3\ 4\ 8\ 7\ 6\ 5\ 9\ 10\ 11\ 12\ 14\ 15\ 13. $$ Puis on compte le nombre d'inversions dans cette suite, c'est-à-dire le nombre de couples d'entiers $(i,j)$ entre 1 et 15 tels que
- $ i > j $,
- le nombre $i$ apparaît avant $j$ dans la liste.
Dans la liste ci-dessus, on a ainsi les inversions $$ (8,7),\ (8,6),\ (8,5),\ (7,6),$$ $$(7,5),\ (6,5),\ (14,13),\ (15,13), $$ et le nombre d'inversions vaut donc 8. En fait, ce qui nous intéresse vraiment, c'est juste de savoir si ce nombre d'inversions est pair ou impair.
Une première observation importante : si on échange deux nombres consécutifs dans une liste, ce qui est appelé saut de mouton dans l'article de Michel Coste, le nombre d'inversions va soit augmenter de 1 (si ces deux nombres étaient dans le bon ordre au début), soit diminuer de 1 (si ils étaient inversés). En effet, les autres couples de nombres restent dans le même ordre dans cette opération. Par exemple, si on échange le $6$ et le $5$ dans la liste ci-dessus, on supprime l'inversion $(6,5)$ ce qui fait diminuer le nombre d'inversions de 1. Au contraire, si on échange le $10$ et le $11$, on ajoute l'inversion $(11,10)$ ce qui augmente le nombre d'inversions d'une unité.
Donc la parité du nombre d'inversions change à chaque saut de mouton. En particulier, puisqu'on passe de la configuration initiale à la configuration visée par un seul saut de mouton (échange du 14 et du 15), ces deux configurations n'ont pas la même parité.
La clé de l'argument repose alors sur cette seconde observation : chaque mouvement autorisé dans le taquin équivaut à un nombre pair de sauts de moutons. Par exemple, si dans la configuration ci-dessous on glisse la plaque 7 vers la case vide en-dessous, cela revient à faire sauter le 7 par-dessus le 6, puis par-dessus le 5, puis par-dessus le 9, puis par-dessus le 10. Donc ce mouvement équivaut à 4 sauts de mouton.
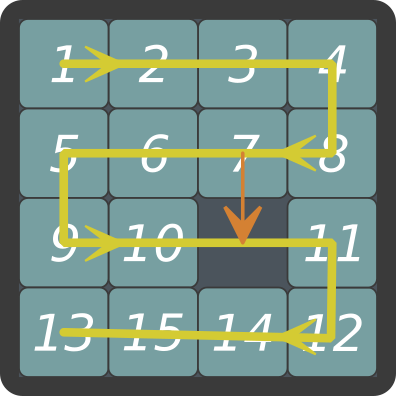
Mais puisque chaque saut de mouton change la parité du nombre d'inversions, un nombre pair de sauts de mouton garde forcément la même parité. Ainsi la parité du nombre d'inversions est un invariant du jeu de taquin.
Comme la configuration initiale du taquin de Sam Loyd et la configuration visée n'ont pas la même parité, le défi proposé par Sam Loyd est impossible à réaliser !
De plus, l'argument reste valable quels que soient les nombres de lignes et colonnes dans la grille. On en conclut que dans le taquin des décimales de $\pi$, il est impossible d'échanger seulement les positions du 6 et du 2.
Pourquoi le taquin des décimales de $\pi$ est-il possible malgré tout ?
Ce qui nous sauve dans le taquin des décimales de $\pi$, c'est la présence de deux plaques portant le même chiffre 1. L'argument de parité du nombre d'inversions montre qu'il est impossible d'échanger seulement les positions du 6 et du 2, cependant il reste tout à fait possible d'échanger le 6 avec le 2 tout en permutant les deux plaques «1». En effet, l'échange des deux «1» change à nouveau la parité du nombre d'inversions de la suite, et donc la nouvelle configuration possède la même parité que celle de départ.
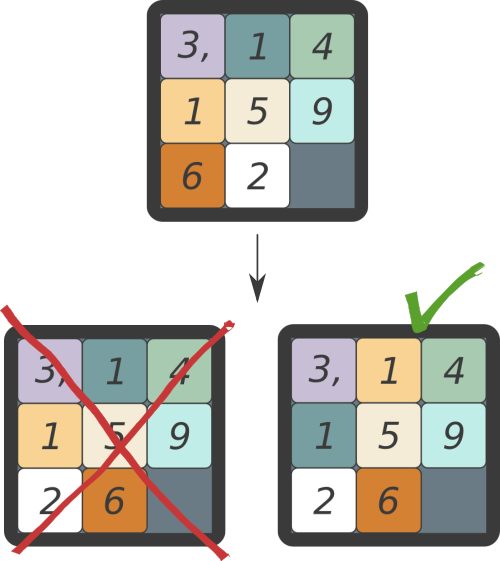
(Attention, dans le taquin des décimales de $\pi$, pour calculer le nombre d'inversions de la suite associée à une configuration donnée il ne faut pas utiliser la liste des chiffres inscrits sur les plaques, puisque le 1 y apparaît deux fois. On peut par exemple numéroter les plaques de 1 à 8 et regarder la liste des numéros le long du chemin dans une configuration donnée.)
Il est expliqué dans cet autre article de Michel Coste (un peu plus technique) que toute configuration possédant la même parité du nombre d'inversions que celle de départ est réalisable avec les mouvements du taquin (cela fonctionne dès qu'il y a au moins 2 lignes et 2 colonnes !).
Et pour ceux qui douteraient encore que le taquin des décimales de $\pi$ a bien une solution, en voici une en 24 coups. Question ouverte : quel est le nombre minimum de coups pour remettre dans l'ordre les décimales de $\pi$ ?
Quelques mots-clés pour aller plus loin
La branche des mathématiques en lien avec ce problème du taquin s'appelle la théorie des groupes. Il s'agit plus précisément ici de l'étude du groupe symétrique, ou groupe des permutations. Les permutations de l'ordre des éléments dans une liste qui ne changent pas la parité du nombre d'inversions forment ce que l'on nomme le groupe alterné. On peut résumer tout ce qui est utilisé ici par cette propriété : les mouvements autorisés dans le taquin engendrent le groupe alterné.