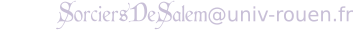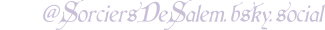Dans notre animation sur l'alignement des planètes, avec les paramètres par défaut on observe certains instants où les planètes adoptent une configuration « en étoile » : elles sont groupées en un nombre fini, variable, de « branches ». Nous allons tenter de comprendre à quels instants on peut observer ce type de configuration étoilées, et d'expliquer l'ordre dans lequel elles se succèdent.

Exemples de configurations en étoile avec 2, 4, 5 et 7 branches.
Description du système présenté dans l'animation
Le système de l'animation est constitué d'un nombre $N$ de planètes qui sont toutes en orbite circulaire autour d'un soleil, dans le même plan orbital. Au départ, c'est-à-dire au temps $t=0$, les planètes sont toutes alignées d'un même côté du soleil.
Position initiale des planètes.
Chaque planète tourne à sa propre vitesse angulaire, qui ne varie pas dans le temps. Dans le choix par défaut des paramètres, ces vitesses angulaires sont choisies de sorte à ce que l'animation présente une période globale $T$, qui en pratique est de 3 minutes : au bout de ce temps, toutes les planètes sont revenues exactement à leur position initiale. La planète 1, la plus éloignée du soleil, est celle qui tourne le moins vite. On note $M$ le nombre de tours qu'elle effectue autour du soleil pendant une période $T$ : $M$ est un nombre entier car, après la période $T$, la planète 1 doit être revenue exactement à sa position initiale.
Ce graphique représente le nombre de tours effectués autour du soleil par la planète 1 en fonction du temps. Puisque la vitesse angulaire est constante, on obtient une droite. Au bout de la période $T$, la planète 1 a effectué un nombre entier $M$ de tours autour du soleil.
On numérote toutes les planètes de la plus éloignée à la plus proche du soleil. Les vitesses angulaires des planètes suivantes sont choisies de telle sorte que, au bout d'une période $T$, chaque planète a fait exactement un tour de plus que la précédente : pendant la durée de la période $T$, la planète 2 effectue $M+1$ tours, la planète 3 un tour de plus que la planète 2 et ainsi de suite. La planète $N$, qui est la plus proche du soleil, effectue donc $M+N-1$ tours autour du soleil pendant la période $T$.
Nombre de tours effectués par chaque planète en fonction du temps.
À la recherche des configurations en étoile
Commençons par bien définir les notions dont nous parlons. Dans la suite, on appelle branche une demi-droite dans le plan orbital dont l'extrémité est au centre du soleil. Une configuration des planètes est dite en étoile si elle est formée de branches comportant chacune plusieurs planètes. Ainsi, la configuration initiale est une configuration en étoile à 1 branche. La figure du début montre d'autres configurations en étoile visibles au cours de l'animation.
Quand deux planètes peuvent-elles se retrouver sur une même branche ?
Analysons la position relative de deux planètes distinctes d'indices $i$ et $j$, et pour cela regardons comment évolue la différence entre les nombres de tours effectués par chacune de ces deux planètes. À $t=0$, cette différence vaut bien sûr 0, et à $t=T$ elle vaut $|j-i|$ puisque la planète la plus proche du soleil aura effectué exactement $|j-i|$ tours de plus que la plus éloignée des deux. Et comme les vitesses angulaires sont constantes, la différence évolue linéairement en fonction du temps. Cette différence prend donc des valeurs entières à tous les instants qui sont des multiples de $\frac{T}{|j-i|}$, et ce sont précisément les instants où les deux planètes $i$ et $j$ se retrouvent sur une même branche. Par exemple, si $|j-i|=3$, entre 0 et $T$ les deux planètes $i$ et $j$ sont situées sur une même branche aux instants 0, $\frac{1}{3}T$, $\frac{2}{3}T$ et $T$.
Ce graphique permet de comparer les nombres de tours effectués par les deux planètes $i$ et $j$ en fonction du temps. Au bout d'une période $T$, la différence entre les deux nombres de tours vaut $|j-i|$. On a mis en évidence les instants où la différence entre les deux nombres de tours prend une valeur entière, qui sont les instants où les deux planètes se retrouvent sur une même branche. La figure correspond au cas où $|j-i|=3$.
Cet argument nous permet d'aboutir à une première conclusion : les configurations étoilées ne peuvent apparaître qu'aux instants $t$ qui s'écrivent sous la forme $t=\frac{a}{b}T$ où $a$ et $b$ sont des nombres entiers. De plus, le dénominateur $b$ de la fraction (mise sous forme irréductible) ne doit pas être trop grand, puisque dans l'étude que nous venons de faire on a $|j-i|\leq N-1$.
Que se passe-t-il aux instants de la forme $\frac{a}{b}T$ ?
Prenons une fraction irréductible $\frac{a}{b}$, dont le dénominateur $b$ est plus petit que le nombre de planètes, et essayons de comprendre la configuration des planètes à l'instant $t=\frac{a}{b}T$. D'après l'analyse ci-dessus, deux planètes $i$ et $j$ sont sur une même branche à l'instant $t$ si et seulement si la fraction $\frac{a}{b}$ peut s'écrire comme une fraction de dénominateur $|j-i|$, c'est-à-dire quand $|j-i|$ est un multiple de $b$. On en déduit que la planète 1 est située sur la même branche que les planètes $1+b$, $1+2b$... De même, la planète 2 est située sur la même branche que les planètes $2+b$, $2+2b$... En continuant ainsi on voit que les planètes 1 à $b$ déterminent $b$ branches différentes sur lesquelles se trouvent toutes les autres planètes : la branche à laquelle appartient une planète $i$ dépend seulement du reste de la division euclidienne de $i$ par $b$. Chacune des $b$ branches porte alors un nombre de planètes qui vaut soit $\lfloor N/b \rfloor$ (la partie entière de $N/b$), soit $\lfloor N/b \rfloor+1$.
Par exemple, à l'instant $t=\frac{1}{2}T$ (la moitié de la période), toutes les planètes d'indice impair se retrouvent sur la même branche que la planète 1, tandis que celles d'indice pair se retrouvent sur la branche de la planète 2 : on obtient 2 branches, qui portent chacune le même nombre de planètes si $N$ est pair, ou respectivement $k+1$ et $k$ planètes si $N$ est de la forme $2k+1$.
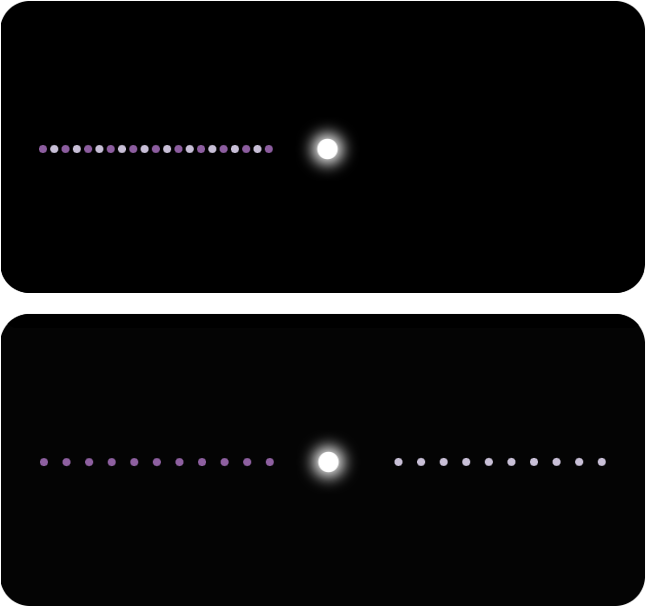
Ici on a coloré les planètes en deux couleur suivant que leur indice est pair ou impair. Dans la position initiale (en haut) on a donc des couleurs alternées sur l'unique branche. À mi-période (en bas), toutes les planètes d'indice pair sont sur une même branche tandis que celles d'indice impair sont sur la branche opposée.
De même, à l'instant $t=\frac{1}{3}T$, toutes les planètes dont l'indice est multiple de 3 se retrouvent sur une même branche, celles dont l'indice est de la forme $3k+1$ se retrouvent sur une deuxième branche, et celles dont l'indice est de la forme $3k+2$ sont alignées sur la 3e branche.
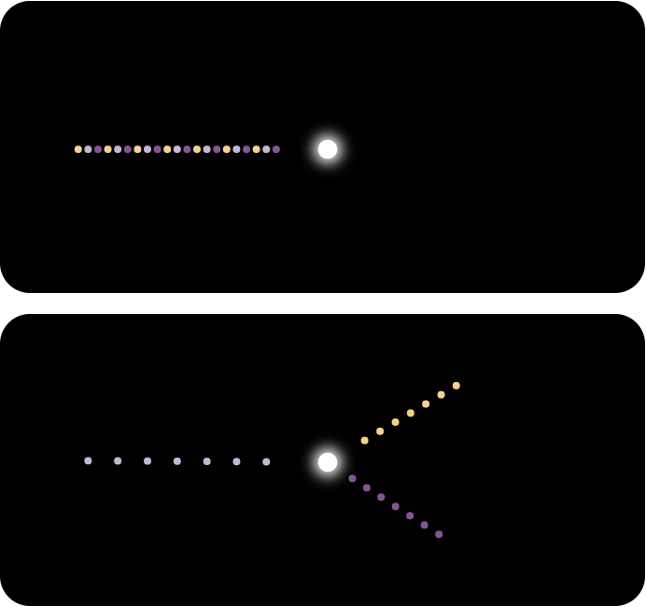
Sur la figure ci-dessus, l'image du haut montre la configuration initiale lorsque les planètes sont coloriées périodiquement avec une période 3. L'image du dessous montre les mêmes planètes dans la configuration en étoile à 3 branches après un temps $T/3$.
L'ordre des étoiles et les suites de Farey
Les branches ne sont bien visibles que si elles comportent suffisamment de planètes. Choisissons arbitrairement de ne considérer que les configurations en étoile dont chaque branche contient au moins 3 planètes : elles correspondent aux fractions irréductibles $\frac{a}{b}$ dont le dénominateur $b$ vaut au plus $N/3$. Dans les paramètres par défaut de l'animation, on a $N=21$ planètes, donc les configurations en étoile dont les branches contiennent au moins 3 planètes sont obtenues aux instants correspondant aux fractions irréductibles dont le dénominateur est inférieur ou égal à 7, c'est-à-dire : $$ \dfrac{0}{1}, \dfrac{1}{7}, \dfrac{1}{6}, \dfrac{1}{5}, \dfrac{1}{4}, \dfrac{2}{7}, \dfrac{1}{3}, \dfrac{2}{5}, \dfrac{3}{7}, \dfrac{1}{2}, \dfrac{4}{7}, \dfrac{3}{5}, \dfrac{2}{3}, \dfrac{5}{7}, \dfrac{3}{4}, \dfrac{4}{5}, \dfrac{5}{6}, \dfrac{6}{7}, \dfrac{1}{1}. $$ Cette suite de fractions écrite dans l'ordre croissant constitue ce que l'on appelle la suite de Farey d'ordre 7. Si on passe à $N=24$ planètes, on va utiliser la suite de Farey d'ordre 8, qui s'obtient en insérant à leur place respective les nouvelles fractions $\frac{1}{8}$, $\frac{3}{8}$, $\frac{5}{8}$ et $\frac{7}{8}$.
À chacune des fractions de cette suite de Farey correspond une configuration en étoile, dont le nombre de branches est donné par le dénominateur de la fraction. Ainsi l'ordre des étoiles est simplement donné par la suite des dénominateurs dans la suite de Farey.
Et si on perturbe un peu les vitesses de rotation ?
Le choix par défaut des vitesses de rotation dans l'animation est très spécifique, et si on modifie même très légèrement ces vitesses on n'observera plus en général le comportement décrit ci-dessus. Si on choisit au hasard des vitesses proches de celles définies par défaut (ce qu'il est possible de faire via le menu des paramètres dans l'animation), voilà ce qu'il va se passer avec probabilité 1 :
- Sauf à la position initiale, on n'observera jamais plus de deux planètes alignées avec le soleil.
- On ne verra donc jamais exactement les configurations en étoile telles qu'elles sont décrites ci-dessus.
- En revanche, si on se donne une configuration arbitraire des planètes, on observera cette configuration de manière approchée infiniment souvent. Par exemple, le système se retrouvera une infinité de fois dans la configuration de départ, à 1 degré près pour chaque planète. Mais, avec 21 planètes et des vitesses de rotation proches de celles par défaut, l'intervalle de temps moyen entre deux telles observations sera de l'ordre de sept milliards de milliards de milliards de milliards d'années !