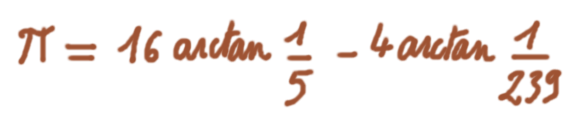Une formule historique
La formule affichée en entête de cette page fut démontrée par le mathématicien anglais John Machin en 1706, et lui permit de devenir le premier homme de l'histoire à calculer les 100 premières décimales du nombre $\pi$.
Bien qu'elle semble tout droit sortie d'un chapeau de sorcier, nous allons expliquer qu'en fait elle est assez simple à démontrer. On peut même obtenir toute une famille de formules du même type en faisant des petits dessins sur du papier quadrillé...
La fonction trigonométrique arctangente
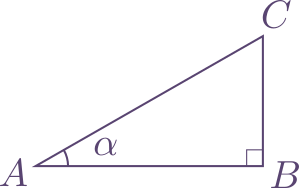
Tout repose sur l'une des formules de base de la trigonométrie que l'on apprend au collège : dans un triangle rectangle comme ci-dessus, la tangente de l'angle $\alpha$ est donnée par $$ \tan\alpha =\frac{BC}{AB}.$$ Par exemple, dans les triangles ci-dessous tracés sur du papier quadrillé, on obtient facilement les tangentes des angles indiqués.

Inversement, la fonction arctangente associe à un nombre $t\ge0$ l'unique angle aigu $\alpha$ tel que $\tan \alpha = t$. Ainsi, sur la figure ci-dessus on a $$\alpha_1=\arctan 1,$$ $$\alpha_2=\arctan\frac{1}{2},$$ $$\alpha_3=\arctan\frac{1}{3}.$$
Mais attention, cette fonction arctangente renvoie toujours la valeur de l'angle exprimée en radians, pas en degrés. Rappelons que la valeur en radians d'un angle est égale à la longueur de l'arc de cercle de rayon 1 intersecté par l'angle.
Par exemple, puisque le périmètre du cercle de rayon 1 vaut $2\pi$, un angle de $360°$ (le tour complet) correspond à $2\pi$ radians. Le demi-tour, $180°$, correspond à $\pi$. L'angle droit mesure, en radians, $\pi/2$, et la moitié de l'angle droit (45°) mesure $\pi/4$.
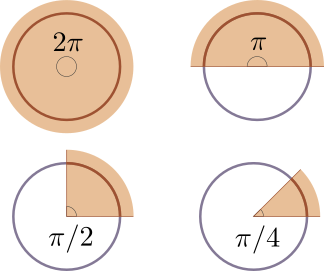
Ce dernier exemple n'est autre que l'angle $\alpha_1$ sur la figure précédente, dont nous avons vu que la tangente vaut 1. On a donc $$ \frac{\pi}{4} = \arctan 1, $$ ce qui nous donne la première formule permettant d'exprimer $\pi$ à l'aide de la fonction arctangente : $$ \pi = 4 \arctan 1. $$
Mais cette première formule n'est pas efficace en pratique pour calculer $\pi$. En effet, pour des raisons que nous expliquerons plus bas, plus le nombre réel $t$ est proche de 0 et plus il est facile de calculer une valeur précise de $\arctan t$. Pour $t=1$ c'est encore trop difficile. L'idée est donc de découper l'angle $\pi/4$ en angles plus petits, que l'on pourra écrire comme des $\arctan t$ pour des nombres $t$ à la fois simples et plus proches de 0.
Deux dessins, deux formules
Traçons un dessin sur du papier quadrillé : cela permet de bien repérer les points à coordonnées entières et de donner facilement la tangente de certains angles. Marquons le point de coordonnées $(3,1)$, et traçons la demi-droite issue de l'origine qui passe par ce point. Elle coupe l'angle de mesure $\pi/4$ en deux angles $\alpha$ et $\beta$ : on a donc ici $$\frac{\pi}{4}=\alpha+\beta.$$
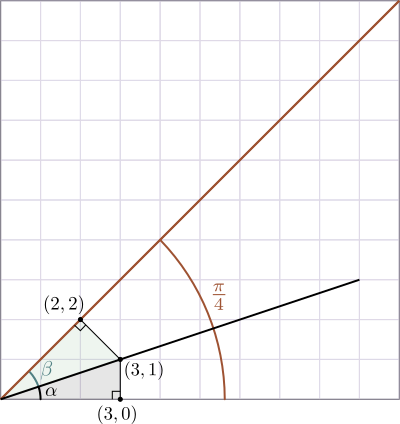
Mais par ailleurs, dans le triangle rectangle du bas on constate que $\tan \alpha = \frac{1}{3}$, car le côté opposé à l'angle $\alpha$ mesure une unité, et le côté adjacent en mesure 3. On a donc $$\alpha=\arctan \frac{1}{3}.$$ Et dans le triangle rectangle du haut, on voit que le côté opposé à l'angle $\beta$ est une diagonale d'un carreau, tandis que le côté adjacent à l'angle $\beta$ est constitué de deux diagonales de carreaux. On a ici $\tan \beta=\frac{1}{2}$, et donc $$\beta=\arctan\frac{1}{2}.$$ En regroupant tous ces résultats, on obtient $\frac{\pi}{4}=\arctan \frac{1}{3}+\arctan\frac{1}{2}$, soit $$ \pi = 4\arctan \frac{1}{3} + 4\arctan\frac{1}{2}.$$ C'est déjà mieux que la première formule, mais essayons de faire un nouveau dessin où tous les angles ont une tangente au plus égale à $\frac{1}{3}$.
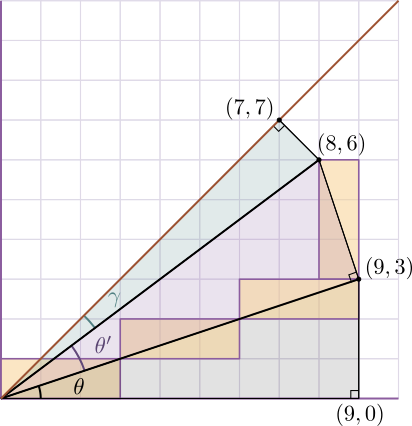
Sur ce nouveau dessin l'angle $\pi/4$ est cette fois découpé en trois angles plus petits : $$ \frac{\pi}{4}=\theta+\theta'+\gamma,$$ où les angles $\theta$, $\theta'$ et $\gamma$ apparaissent au sommet de trois nouveaux triangles rectangles. Dans celui du bas, on voit que $\tan\theta=\frac{1}{3}$ puisque le côté opposé à $\theta$ mesure 3 unités tandis que le côté adjacent en mesure 9. donc $$\theta=\arctan\frac{1}{3}.$$ Dans le deuxième triangle rectangle, il est facile également de calculer $\tan\theta'$ : le côté opposé à $\theta'$ est la diagonale d'un rectangle $3\times 1$, et le côté adjacent est constitué de 3 telles diagonales. On obtient $\tan\theta'=\frac{1}{3}$, et donc aussi $$\theta'=\arctan\frac{1}{3}.$$ Enfin dans le triangle rectangle du haut, le côté opposé à $\gamma$ est la diagonale d'un carreau, et le côté adjacent est constitué de 7 diagonales de carreaux. Cela nous donne $$ \gamma = \arctan\frac{1}{7},$$ et la formule correspondant au deuxième dessin est donc $$ \pi = 8\arctan\frac{1}{3} + 4 \arctan\frac{1}{7}. $$
Preuve de la formule de Machin
La formule de Machin peut s'écrire sous la forme $$ \frac{\pi}{4} = 4 \arctan \frac{1}{5} - \arctan\frac{1}{239}.$$ On devine avec les deux exemples précédents qu'une telle formule va s'obtenir avec un dessin du même type, mais où cette fois on fera intervenir 4 angles de mesure $\arctan \frac{1}{5}$. Voici une façon assez générale de tracer un tel angle sur du papier à carreaux.
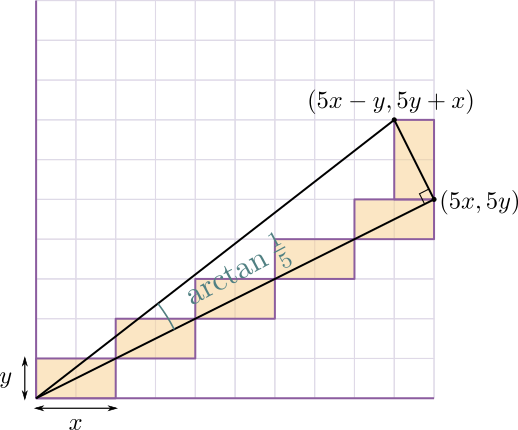
Pour $x$ et $y$ entiers positifs ou nuls, on considère le triangle formé par l'origine, le point de coordonnées $(5x,5y)$ et celui de coordonnées $(5x-y,5y+x)$. C'est un triangle rectangle, dont l'angle à l'origine à pour tangente $\frac{1}{5}$. En effet le côté opposé à l'angle est la diagonale d'un rectangle de dimensions $x\times y$, et le côté adjacent est constitué de 5 telles diagonales.
En partant d'un premier point sur l'axe des abscisses, c'est-à-dire de coordonnées $(5x,0)$ dans cette construction, on obtient comme coordonnées du second point $(5x,x)$, et cela nous donne un premier angle de tangente $\frac{1}{5}$. La construction peut être répétée pour obtenir un deuxième angle de même mesure tout en restant avec des points à coordonnées entières à condition que $x$ soit multiple de 5, c'est-à-dire que l'abscisse du premier point soit divisible par 25.
La formule de Machin faisant intervenir 4 angles de tangente $\frac{1}{5}$, on doit s'arranger pour pouvoir répéter la construction quatre fois de suite. Pour cela, on a besoin d'un point de départ dont l'abscisse est quatre fois divisible par 5, c'est-à-dire divisible par $5^4=625$. On part donc du point de coordonnées $(625,0)$, et on applique 4 fois la construction de $\arctan \frac{1}{5}$ expliquée ci-dessus. On obtient ainsi 4 nouveaux points dont les coordonnées successives sont
- $(625,625/5)=(625,125)$,
- $(625-125/5,125+625/5)=(600,250)$,
- $(600-250/5,250+600/5)=(550,370)$,
- $(550-370/5,370+550/5)=(476,480)$.
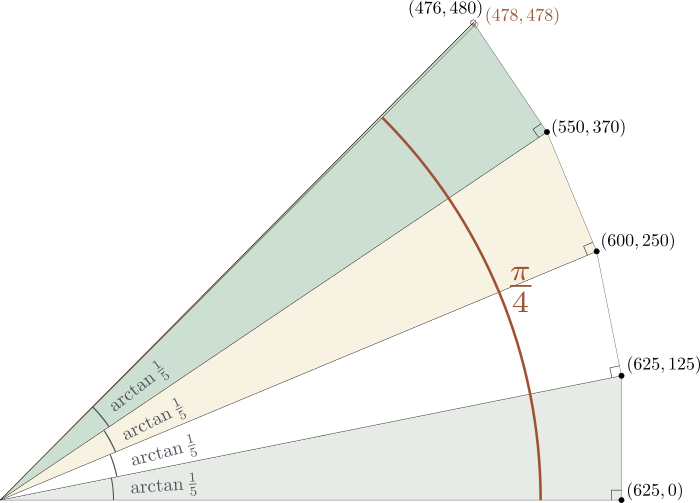
Ces 5 points forment avec l'origine 4 triangles rectangles, et dans chacun de ces triangles l'angle à l'origine a pour tangente $\frac{1}{5}$. Le cinquième point est très légèrement au-dessus de la demi-droite qui forme l'angle $\pi/4$ avec l'axe des abscisses. Ainsi $4 \arctan\frac{1}{5}$ est légèrement plus grand que $\pi/4$. Pour mesurer exactement de combien on a dépassé, on considère un dernier triangle rectangle formé par l'origine, le dernier point obtenu de coordonnées $(476,480)$, et le point de coordonnées $(478,478)$, qui lui est sur la demi-droite formant l'angle $\pi/4$.
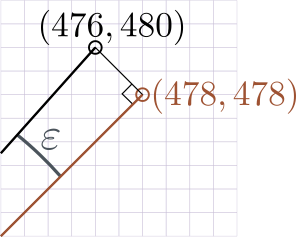
Appelons $\varepsilon$ l'angle à l'origine dans ce triangle. Le côté opposé à cet angle est formé de deux diagonales de carreaux, tandis que le côté adjacent est constitué de 478 diagonales de carreaux. On a donc $$\tan\varepsilon=\frac{2}{478}=\frac{1}{239},$$ c'est-à-dire $$\varepsilon=\arctan\frac{1}{239},$$ ce qui conclut la preuve de la formule de Machin.
Les décimales de $\pi$ par le développement de la fonction arctangente
Comment la formule de Machin a-t-elle permis le calcul des 100 premières décimales de $\pi$ à une époque où l'on ne disposait pas de machine à calculer ou d'ordinateur ? L'outil essentiel est ce que l'on appelle le développement en série entière de $\arctan t$. Pour $t\in[-1,1]$, $\arctan t$ peut se calculer comme la somme infinie suivante : $$ \arctan t = t - \frac{t^3}{3} + \frac{t^5}{5} - \frac{t^7}{7} +\cdots = \sum_{k=0}^{\infty} (-1)^k \frac{t^{2k+1}}{2k+1}. $$ Bien sûr, en pratique on ne peut calculer que des sommes finies, mais cette formule signifie que si on ajoute suffisamment de termes de la somme, on peut s'approcher aussi bien que l'on veut de $\arctan t$.
Par exemple pour $t=1$ on obtient $\frac{\pi}{4}=\arctan 1=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$, soit $$ \pi = 4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots\right).$$ (Formule donnée par Leibniz au dix-septième siècle.) Bien que très simple, cette formule n'est pas efficace pour obtenir une valeur approchée acceptable de $\pi$ car la convergence de la série est ici très lente : il faudrait additionner un nombre déraisonnable de termes pour on veut obtenir une bonne précision. Ainsi, en sommant les 100 premiers termes de la série, on obtient comme valeur approchée de $\pi$ $$ 4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots+\frac{1}{197}-\frac{1}{199}\right) \simeq \mathbf{3,1}5169.$$ En sommant un million de termes (ce qui n'est pas faisable sans ordinateur !), on n'obtient que quelques décimales exactes : $$ 4\left(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots+\frac{1}{1\,999\,997}-\frac{1}{1\,999\,999}\right) \simeq \mathbf{3,14159}36.$$
Pour accélérer la convergence, et donc n'avoir qu'un nombre raisonnable de termes à additionner, il est judicieux d'utiliser une formule dans laquelle intervient $\arctan t$ pour des valeurs de $t$ plus proches de 0. En effet plus $t$ est proche de 0 et plus la série converge rapidement. C'est la raison pour laquelle la formule de Machin est beaucoup plus efficace. Elle se traduit par \begin{align} \pi = & 16\left(\frac{1}{5}-\frac{1}{3\times 5^3}+\frac{1}{5\times 5^5}-\frac{1}{7\times 5^7}+\cdots\right)\\ & -4\left(\frac{1}{239}-\frac{1}{3\times 239^3}+\frac{1}{5\times 239^5}-\frac{1}{7\times 239^7}+\cdots\right). \end{align} En ne sommant que les 8 termes explicites dans la formule ci-dessus, on obtient environ $\mathbf{3,141}621$ comme valeur approchée de $\pi$. En ajoutant seulement 2 termes supplémentaires dans la première série (celle du développement de $\arctan\frac{1}{5}$, qui converge le moins rapidement), on gagne plusieurs décimales avec la nouvelle valeur approchée $\pi\simeq \mathbf{3,1415926}82$.
Aller à la page regroupant les activités autour du nombre $\pi$.