Objectif : le même nombre $\pi$ pour le périmètre et l'aire ?
Le nombre $\pi$ est défini comme le rapport entre le périmètre d'un cercle et son diamètre : ce rapport est constant, il ne dépent pas du cercle choisi. Dans son traité intitulé De la mesure du cercle, l'illustre scientifique Archimède de Syracuse (287 à 212 avant JC) montre que la même constante intervient également lorsque l'on fait le rapport entre l'aire d'un disque et le carré du rayon.
Nous présentons ci-dessous une méthode géométrique pour comprendre le lien entre l'aire du disque et le périmètre du cercle.
Méthode : le partage de la pizza
Considèrons une pizza en forme de disque de rayon $R$. Son périmètre est $2\times R\times \pi$. Justifions maintenant que son aire s'exprime à l'aide de la même constante $\pi$, et vaut $\pi \times R \times R$.
On coupe d'abord la pizza en deux suivant un diamètre, puis on partage chaque demi-pizza en un grand nombre de parts de même taille.

Chaque part de pizza a presque la forme d'un triangle : c'est une figure géométrique dont deux côtés sont des segments de longueur le rayon de la pizza, et le dernier côté est un petit arc de cercle. Plus le nombre de parts est grand, plus ces parts ressemblent à des triangles car l'arc de cercle devient assimilable à un petit segment de droite.
On réarrange maintenant les morceaux de la manière suivante.
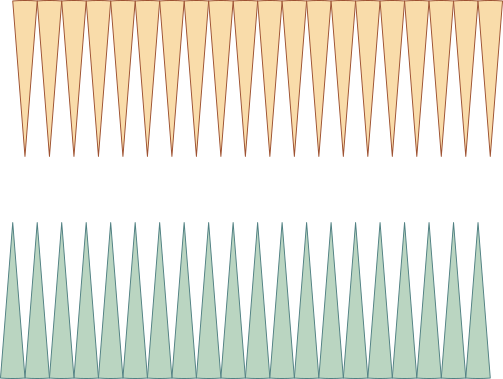
puis
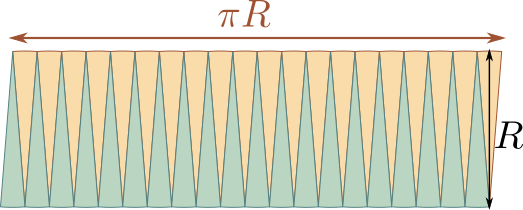
On obtient ainsi une nouvelle forme de pizza, qui coïncide presque avec un rectangle. La largeur de ce rectangle est le rayon $R$ de la pizza initiale, et sa longueur est le demi-périmètre $\pi \times R$. Il a donc pour aire $\pi \times R \times R=\pi R^2$. Or la nouvelle pizza a gardé la même aire que le disque de départ. Ce disque a donc également pour aire $\pi R^2$.
L'animation ci-dessous permet de visualiser le réarrangement des parts de pizza.
La $\pi$izza de Léonard ?
Si Archimède a bien montré que le même nombre $\pi$ apparaît dans la formule donnant le périmètre du cercle et dans celle donnant l'aire du disque, sa méthode ne consistait pas à réarranger les parts de pizza. On peut trouver une présentation de l'argument d'Archimède dans cet article de la revue Accromath.
Nous ne savons pas qui le premier a eu l'idée du découpage présenté ci-dessus, mais cela remonte au moins à Léonard de Vinci, comme en témoigne ce détail du Codex Atlanticus datant de 1513 :

Aller à la page regroupant les activités autour du nombre $\pi$.