En complément du poster «Les maths ça sert à rien (sauf à...)» téléchargeable ici, nous vous proposons quelques pistes pour aller plus loin...
Comme pour le poster, il ne s'agit pas ici de donner une liste exhaustive des applications des mathématiques, ce qui serait évidemment impossible. Le but est simplement de donner quelques exemples, certains bien connus et d'autres moins, de domaines où les mathématiques interviennent de façon essentielle.
Nous espérons compléter prochainement la liste des thèmes abordés.
Comprendre la course des étoiles

Depuis des millénaires les progrès de l'astronomie sont profondément liés à ceux des mathématiques. L'observation des astres et les questions qui en découlent sont une motivation majeure pour le développement d'outils mathématiques, de la géométrie classique (trigonométrie pour repérer les positions des corps célestes, coniques pour décrire leurs mouvements...) au calcul différentiel qui permit à Isaac Newton de formuler les lois de la mécanique classique. En étudiant des problèmes de mécanique célestes, Henri Poincaré a posé les fondements de la théorie moderne des systèmes dynamiques et entrevu la notion de chaos. Albert Einstein s'appuie lui sur le concept de variété géométrique introduit par Bernhard Riemann pour développer la théorie de la relativité, expliquant notamment certaines anomalies dans les observations astronomiques.
Les références sur les liens entre mathématiques et astronomie sont innombrables. En voici quelques unes :
- Tangente HS n°21 «L'astronomie : la géométrie de l'univers» (Éditions POLE, 2005)
- Accromath : dossier Mathématiques et Astronomie
- Une vidéo expliquant la loi des aires de Kepler
Prévoir le temps qu'il fera

Préoccupation majeure des hommes depuis toujours, les prévisions météorologiques ont longtemps reposé sur des dictons plus ou moins fondés. Depuis l'avènement des ordinateurs, elles sont désormais basées sur la prévision numérique du temps. Comme expliqué dans cet article tiré de la brochure L'explosion des mathématiques, il s'agit de résoudre numériquement les équations de la dynamique des fluides régissant l'évolution de l'atmosphère ou des océans. Le principe est simple : en connaissant parfaitement l'état de l'atmosphère et des océans aujourd'hui, et en faisant tourner ces équations à partir de ces conditions initiales, on devrait pouvoir prédire l'évolution de la situation météorologique dans les jours à venir. Malheureusement des obstacles de taille rendent difficiles l'application de cette idée :
- on ne dispose évidemment pas de capteurs en tous les points du globe, et il faut donc reconstruire au mieux l'état initial en fonctions des informations partielles dont on dispose,
- si puissants soient-ils, les ordinateurs ne peuvent que résoudre approximativement les équations physique, en discrétisant à la fois le temps et l'espace sous forme d'un maillage.
La situation est d'autant plus critique que, comme l'a montré le météorologue Edward Lorenz en 1963, même un modèle extrêmement simplifié de l'évolution de l'atmosphère se comporte de façon chaotique et montre une très grande sensibilité aux conditions initiales. C'est ce phénomène qu'il a popularisé quelques années plus tard sous le fameux nom d'effet papillon.
Les mathématiques interviennent à tous les niveaux pour optimiser les prévisions. L'analyse numérique s'attache à toujours améliorer le compromis rapidité/précision de la résolution numérique des équations physiques. L'utilisation de méthodes statistiques permet également de corriger certaines erreurs de façon efficace.
Mesurer le monde
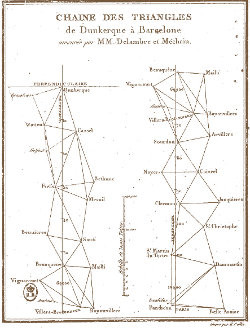
Dès l'antiquité les scientifiques ont employé des outils de géométrie (étymologiquement « mesure de la Terre ») pour mesurer le monde qui les entoure. Outre le légendaire épisode de Thalès mesurant la hauteur de la pyramide de Khéops à l'aide de son fameux théorème, on peut surtout penser à l'estimation de la circonférence de la Terre par Ératosthène. Il obtient déjà une très bonne approximation, ce qui est remarquable étant donné les moyens rudimentaires employés : Ératosthène estime la distance entre les villes d'Alexandrie et Syène via le temps mis par un chameau pour aller d'une ville à l'autre ! Depuis, des méthodes plus précises ont été mises au point pour mesurer la distance entre deux points éloignés, notamment la triangulation (voir aussi cet article d'Images des Mathématiques).
Au début du dix-neuvième siècle, l'illustre mathématicien Carl Friedrich Gauss entreprend une étude géodésique de l'état de Hanovre qui le conduira à développer sa théorie de la courbure des surfaces, incluant notamment le theorema egregium (« théorème remarquable »).
Aujourd'hui on mesure la terre au centimètre près depuis l'espace en utilisant des systèmes comme le GPS, mais là aussi l'emploi d'outils mathématiques est fondamental. Et même lorsque l'on connaît parfaitement les mesures de la Terre se posent encore des problèmes mathématiques difficiles liés à la représentation du monde sous forme de cartes.
Partager équitablement

Pour l'élève de l'école primaire ou du collège, certaines notions mathématiques comme la division ou les fractions sont naturellement introduites en lien avec des problèmes de partage. La géométrie elle-même trouverait son origine dans le partage des terres cultivables dans l'Égypte antique (voir la brève de maths « Partager la terre »). La résolution d'autres problèmes de partage fait parfois appel à des résultats mathématiques profonds : c'est le cas par exemple du problème du partage du collier, issu de problèmes d'optimisation sur des chaînes de montage. Il s'agit de partager équitablement un collier comportant plusieurs types de perles entre les voleurs qui l'ont dérobé, en le coupant le moins de fois possible. Sa résolution fait intervenir le théorème de Borsuk-Ulam. On peut également citer l'utilisation du lemme combinatoire de Sperner dans des problèmes de partages équitables formulés en théorie des jeux (voir par exemple comment partager équitablement le loyer d'une colocation).
Protéger nos secrets

Comment transmettre un message en ne permettant qu'à son seul destinataire d'y avoir accès est une question qui préoccupe les militaires et les diplomates depuis des millénaires, et qui s'accompagne inévitablement de l'autre question non moins cruciale : comment décoder un message crypté de l'ennemi ? La concurrence entre ces deux problèmes a entraîné le développement de systèmes de codage de plus en plus élaborés, du codage de César à la machine Enigma des allemands pendant la seconde guerre mondiale. Dans cette vidéo de Science Étonnante ainsi que dans cet article d'Images des Mathématiques, on explique comment les mathématiques jouent un grand rôle dans cette question.
Aujourd'hui la croissance exponentielle des informations privées transmises sur internet fait des questions de cryptographie un problème qui nous concerne tous au quotidien. Cet autre article d'Images des Mathématiques explique de manière accessible la problématique des clés publiques et privées, utilisées dans la cryptographie asymétrique (voir aussi sur cet article d')i(nterstices). Lorsqu'en 1640 Pierre de Fermat énonça son petit théorème en arithmétique modulaire, il ne s'imaginait certainement pas que, quelques siècles plus tard, ce théorème serait à la base d'un algorithme de cryptographie asymétrique utilisé par des milliards d'internautes. Cet algorithme porte le nom de RSA, du nom de ses inventeurs Ron Rivest, Adi Shamir et Len Adelman. Son efficacité repose sur le fait qu'il est très facile (pour un ordinateur) de multiplier entre eux deux nombres premiers très grands, mais très difficile de retrouver ces deux nombres quand on connaît seulement leur produit. Des présentations de RSA se trouvent sur cet article de Science Étonnante ou celui ci d')i(nterstices.
Si le codage RSA fonctionne parfaitement depuis des années, ce n'est pas pour autant la fin de la recherche d'autres systèmes de cryptage. L'arrivée annoncée dans un futur plus ou moins proche des ordinateurs quantiques pose un véritable défi : ces ordinateurs seront en effet potentiellement capables de factoriser rapidement un très grand nombre en produit de facteurs premiers, et donc de casser le codage RSA. Heureusement des problèmes mathématiques encore plus difficiles à résoudre que la factorisation en nombres premiers ne manquent pas, et certains sont envisagés dans ce que l'on nomme par anticipation la cryptographie post-quantique. C'est par exemple le cas de questions relatives aux réseaux euclidiens.
Écouter de la musique

Les liens entre mathématiques et musique semblent aussi anciens que les mathématiques elles-mêmes : pour les grecs de l'antiquité, la musique fait partie du quadrivium des sciences mathématiques, avec l'arithmétique, l'astronomie et la géométrie. On trouve de nombreux documents, par exemple cette vidéo, sur les problèmes arithmétiques posés par la construction de gammes musicales harmonieuses. Comme on le voit dans cette autre vidéo, les mathématiques permettent également d'analyser les rythmes musicaux, et même de composer des improvisations à l'aide de modèles aléatoires ! Le son produit par un instrument de musique est lié aux solutions mathématiques d'un problème physique appelé « équation des ondes », présenté dans cet article.
La musique que l'on écoute aujourd'hui est le plus souvent diffusée par le biais de canaux numériques, qui nécessitent également de nombreux outils mathématiques pour coder efficacement le son. C'est notamment le cas du fameux codage MP3 qui, à l'instar du codage JPEG pour les photographies (voir plus loin), utilise une variante de la transformée de Fourier (la transformée en cosinus discrète) pour éliminer des informations non nécessaires à la qualité de l'écoute, puis une technique de compression appelée codage de Huffman.
Décrypter le big data

Il est un phénomène auquel on peut aujourd'hui difficilement échapper : les données numériques sont partout ! L'explosion des moyens de collecte et de stockage ainsi que l'apparition d'objets connectés munis de capteurs multiples les rendent omniprésentes. Cela ne concerne pas seulement les fameux GAFA, mais bien tous les secteurs d'activités et de recherche : industrie pharmaceutique et monde médical, bioinformatique et génomique, secteur bancaire et assurance, commerce, météorologie et astronomie, mais aussi sciences sociales. Tous nos mouvements, actions et documents sont désormais susceptibles d'être indexés, numérisés, stockés ! Notre capacité à valoriser, exploiter mais aussi protéger cette nouvelle richesse est donc un défi crucial pour le XXIe siècle.
Le terme « big data » ou « méga-données » couvre ce phénomène récent. De nos jours, les données sont hétérogènes (de format et de nature variée : textes, images, nombres, signaux...), volumineuses (grand nombre d'observations, et observations de très grande dimension), et souvent collectées de manière fortuite (pas seulement générées volontairement). Sur quelles disciplines peut-on se baser pour décrypter ces masses de données ? Si la statistique, dont un des objectifs (ou en tant que partie des mathématiques proposant des modèles probabilistes) est de proposer des modèles mathématiques pour la collecte, l'organisation, l'analyse et la compréhension de données apparaît bien sûr en première ligne, les méthodes classiques sont inopérantes au vu des caractéristiques ci-dessus. Elles se confrontent en particulier au fléau ou à la malédiction de la dimension, le volume des données étant une fonction exponentielle de la dimension.
Une approche transdisciplinaire, permettant la mise en œuvre de méthodes numériques sophistiquées, au croisement des mathématiques, de l'informatique, et même de la physique est requise et s'est développée peu à peu : c'est l'émergence de la « science des données » (« data science », et du métier associé de « data scientist »). Censée permettre une exploitation des données comme un tout, elle suscite le développement de nombreuses initiatives, en recherche et en enseignement.
Certaines méthodes algorithmiques se révèlent aujourd'hui extrêmement fructueuses en pratique : on peut penser aux réseaux de neurones profonds, le fameux « deep learning », pour la reconnaissance d'images sur d'énormes bases de données. Cependant, l'implication des mathématiques dans le secteur des big data, via la statistique mais aussi la théorie de l'approximation ou l'optimisation, reste bien sûr un challenge très important pour valider les découvertes.
Diagnostiquer et soigner plus efficacement
La première utilisation de modèles mathématiques en médecine est généralement attribuée à Daniel Bernoulli. Dans son Essai d’une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l’inoculation pour la prévenir (1760), il profite du développement du calcul infinitésimal pour proposer des équations différentielles dont l'analyse permet de se prononcer en faveur de l'inoculation du virus de la variole. C'est la naissance de l'épidémiologie. Depuis, cette discipline, qui a pour objectif l'étude de la répartition et des déterminants des maladies dans une population, n'a cessé d'influer sur les politiques de santé publique, pour établir les mesures de prévention et les recommandations vaccinales.
On distingue généralement l'épidémiologie analytique, de l'épidémiologie descriptive. La première vise à identifier les principaux facteurs de risque des maladies, comme les cancers. L'épidémiologie descriptive, quant à elle, s'intéresse à la naissance et la propagation des épidémies : à l'origine le paludisme (Sir Ronald Ross, 1911), puis Ebola, grippes (H1N1...), VIH, SRAS, tuberculose, et plus récemment COVID-19. Si les enquêtes statistiques y ont une place fondamentale (comme pour l'épidémiologie analytique), la modélisation joue un rôle clé. Les modèles les plus étudiés sont dits compartimentaux. Ils séparent les individus en différentes catégories (les compartiments), et peuvent être déterministes (équations différentielles), ou probabilistes (processus de branchement). Différents indicateurs sont considérés, notamment le fameux R0, qui est le nombre moyen de personnes à qui un malade transmet le virus (voir cette conférence ou cette interview à propos du COVID 19, ou cet article d'Images des Mathématiques), et le taux de mortalité.
L'épidémiologie n'est pas le seul champ où mathématiques et médecine interagissent. De plus en plus se développent des modèles permettant de schématiser les phénomènes biologiques. La mécanique des fluides, le calcul scientifique et l'analyse numérique fournissent des équations pour le système respiratoire, les écoulements sanguins, tandis que les probabilités (en particulier des processus stochastiques appelés processus de Hawkes) sont par exemple utilisées pour représenter l'activité neuronale.
Contribution la plus connue des mathématiques en médecine et pharmacie, les outils de la statistique sont utilisés pour valider les résultats des recherches. Les tests d'hypothèses sont au cœur de la mise sur le marché de nouveaux médicaments, et les modèles statistiques permettent en pharmaco-cinétique l'étude de la réponse d'un organisme à un traitement. D'autres modèles encore permettent l'optimisation individuelle des thérapies anticancéreuses, en équilibrant les critères d'efficacité avec la toxicité (voir cette conférence, ou cet article de The Conversation).
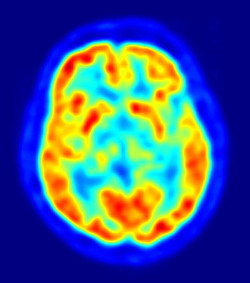
Les mathématiques (traitement du signal) sont aussi derrière l'imagerie médicale (tomodensitométrie, IRM, TEP-Scan). La première question posée est celle de la reconstruction des images, à partir de certaines mesures : c'est ce qu'on appelle un problème inverse. La théorie de Radon permet par exemple de reconstruire une image de scanner, à partir de mesures de l'énergie de rayons X absorbée par l'organisme. Se pose ensuite la question de l'interprétation des images obtenues, et là encore, les mathématiques apportent leur éclairage : comparaison d'image à des cartographies de référence ou ciblage d'opérations chirurgicales. Enfin, les méthodes récentes d'apprentissage automatique peuvent servir d'aide au diagnostic : un ordinateur peut être entraîné sur de grandes bases d'images pour détecter, aussi bien qu'un clinicien à l'œil nu, des tumeurs cancéreuses.
Les mathématiques ont donc beaucoup à apporter à la médecine, aussi bien pour prévenir, diagnostiquer et soigner plus efficacement. Encore plus peut-être dans ce domaine que dans d'autres, les mathématiciens travaillent (ou doivent travailler) en étroite collaboration avec les médecins et biologistes, pour construire les modèles les plus raisonnables possibles, mettre en œuvre des démarches raisonnées de validation des traitements, être prudent sur l'interprétation de certains résultats. Cela ne les empêche pourtant pas de se retrouver au cœur de certaines polémiques : citons par exemple les débats récents sur les OGM ou l'affaire dite des bébés sans bras.
Photographier les papillons

Depuis les années 2000 les appareils photos numériques ont peu à peu remplacé les pellicules argentiques, les photographies sont devenues des suites de nombres, et la chimie qui permettait le développement des photos a laissé la place au traitement numérique des images. À chaque étape de la vie d'une photographie, des calculs mathématiques très avancés sont effectués par l'appareil ou l'ordinateur. Ainsi au moment d'enregistrer la photo sur la carte mémoire, différents outils mathématiques sont employés afin de réduire efficacement la taille du fichier sans compromettre la qualité de l'image : dans la compression JPEG, on utilise principalement la transformée en cosinus discrète et le codage de Huffman (comme le codage MP3 présenté ci-dessus). On peut également par la suite souhaiter modifier la photographie pour la rendre plus contrastée, plus nette, ou éliminer certains de ses défauts, et cela implique également des calculs sur les pixels de l'image. À titre d'exemple, on peut voir sur cet article d'Image des Mathématiques comment le traitement numérique des pixels permet de restaurer des vieux films.
Décoder l'ADN

La découverte de la molécule d'ADN, vecteur de l'hérédité, date des années 1950. Pourtant, les liens étroits entre les mathématiques et la génétique sont bien plus anciens.
On peut par exemple faire remonter aux travaux de Francis Galton l'origine de la droite de régression, cruciale en statistique : ce cousin de Darwin a pour la première fois employé le terme en étudiant le lien entre la taille des individus et celle de leurs parents. Les lois de Mendel font ensuite entrer les probabilités dans le champs de la génétique, en définissant la manière dont les allèles (formes d'un même gène) se transmettent de génération en génération. Depuis, les relations entre les différents champs de la génétique et les mathématiques de l'aléatoire (probabilités, statistique) n'ont cessé de se développer.
La génétique des populations a pour objectif d'étudier la diversité et la variabilité génétique des populations, à travers les âges et en différents lieux. Elle se fonde sur des modèles mathématiques probabilistes, représentations simplifiées et imparfaites de la réalité mais permettant des prédictions ou des vérifications d'hypothèses biologiques. L'un des plus simples est le modèle de Wright-Fisher, qui décrit l'évolution d'une population dans laquelle chaque individu a un seul parent, et dont on peut ainsi reconstruire la généalogie. Si on imagine que la population devient infinie, on aboutit à un modèle limite célèbre en écologie et très étudié en probabilité, le coalescent de Kingman.
L'épidémiologie génétique s'intéresse quant à elle à la détermination des facteurs génétiques intervenant dans l'apparition des maladies et influençant les traits humains. Il s'agit d'identifier les gènes impliqués dans une maladie, estimer les risques liés aux différents génotypes ou encore évaluer leurs interactions, via des méthodes statistiques telles l'analyse de liaison ou les tests d'associations.
Un tournant a lieu à la fin des années 1970, avec, parallèlement aux développements des recherches sur les domaines précédents, l'émergence de la biologie à haut débit et la bioinformatique : les progrès technologiques ainsi que l'alliance de la biologie et de l'informatique permettent de décrypter de manière systématique les séquences biologiques à l'échelle moléculaire (ADN, mais aussi les ARN). C'est l'avènement de la génomique. Le séquençage aboutit à de longs « textes » écrits dans un alphabet de 4 lettres (les nucléotides, A, T, C, G pour l'ADN) qui sont autant de données de grande dimension à décoder pour les statisticiens. Si la modélisation classique utilise généralement des chaînes de Markov (prise en compte la dépendance entre 2 lettres successives), les questions associées sont multiples : détection de régions codantes ou non), analyse de l'expression des gènes, recherche de mots de fréquence exceptionnelle dans les génomes, inférence des mécanismes de régulation de gènes via des graphes... Les progrès de l'intelligence artificielle devraient aussi permettre une exploration systématique de ces « big data » de la santé dans les années à venir, et révolutionner à nouveau tant la génomique que l'épidémiologie génétique.
Enfin, les probabilités et la statistique ne sont pas les deux seules branches des mathématiques en lien avec la génétique : le séquençage individuel se développant à grande vitesse, se pose la question de la sécurité des données génétiques des individus par des méthodes de cryptographie. Par ailleurs, le code source des célèbres automates cellulaires se comporte comme un brin d'ADN, et permet une modélisation simple du vivant. Ces entités virtuelles, inventées par le mathématicien Von Neumann avant même la découverte de la molécule d'ADN, sont toujours étudiées aujourd'hui. L'un des plus célèbres automates cellulaires, dû au mathématicien John Conway, s'appelle d'ailleurs le jeu de la vie!
Améliorer les performances sportives

On pourrait imaginer que les mathématiques n'ont rien à voir avec le sport. Pourtant, même dans ce domaine elles interviennent à de multiples niveaux. Naturellement, on a besoin de résoudre des problèmes combinatoires parfois difficiles pour organiser des tournois en respectant des contraintes parfois compliquées. On peut penser aussi aux méthodes pour classer les différents compétiteurs ou équipes, qui elles aussi font appel à des outils mathématiques de plus en plus évolués. De manière moins évidentes, les mathématiques sont également présentes dans le choix des stratégies des joueurs: savez-vous par exemple que le tireur de pénalty, tout comme le gardien qui veut empêcher le ballon de rentrer, peuvent optimiser leurs chances de succès en recourant aux équilibres préconisés par la théorie des jeux ? Ce champ des mathématiques très utilisé en économie a donc aussi des applications dans le sport ! Les entraîneurs et préparateurs sportifs ont aussi recours à la science des données pour traiter les informations collectées au cours des compétitions, de plus en plus nombreuses. (Voir aussi cette vidéo de Math Park sur l'utilisation des statistiques dans le basket.) Enfin les mathématiques sont également employées dans l'amélioration de la technique même du sportif. Elles servent ainsi à modéliser et mieux comprendre les mouvements, mais aussi à optimiser la gestion de l'effort au cours d'une course. Sur ce thème on peut également regarder la vidéo La physique du rugby du séminaire Math Park.