Est-il possible de calculer la somme de deux nombres en ne connaissant qu'un seul de ces deux nombres ? Cela paraît incroyable, mais pourtant dans certaines circonstances on peut le faire ! C'est ce que l'on va voir grâce à ce tour de magie basé sur les propriétés des nombres de Fibonacci.
Déroulement du tour
Au préalable, télécharger et imprimer cette fiche
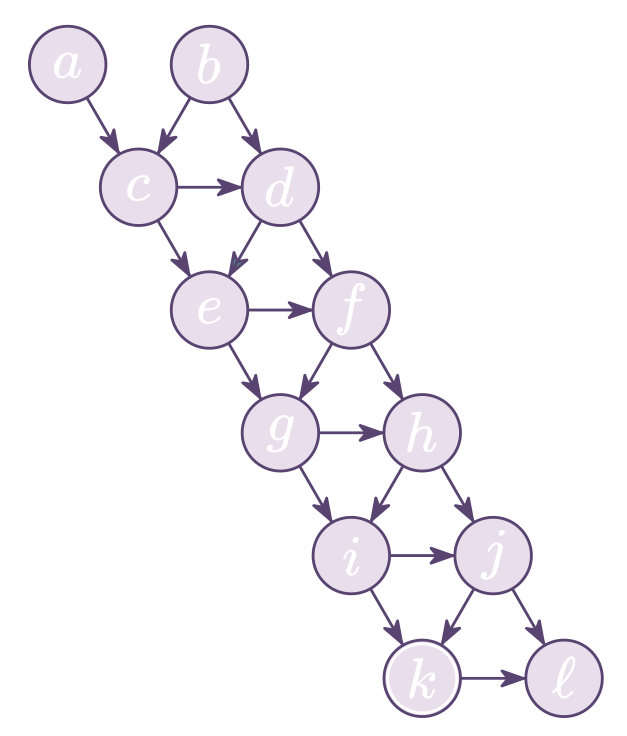
Donner cette fiche à une personne volontaire dans le public. Cette personne choisit sans les divulguer deux nombres entiers $a$ et $b$ entre 1 et 20. Elle les écrit dans les deux premières cellules en haut de la fiche. Puis elle est invitée à compléter les cellules suivantes successivement en calculant à chaque fois la somme des deux derniers nombres écrits : elle commence donc par calculer $c=a+b$, puis $d=b+c$, $e=c+d$, et ainsi de suite jusqu'à $$ \ell=j+k, $$ mais ceci sans jamais donner d'information sur les nombres écrits. Lorsque la fiche est complètement remplie, la personne volontaire communique seulement le nombre $k$ écrit dans l'avant-dernière case.
La personne qui présente le tour annonce alors qu'elle va calculer le dernier nombre $\ell$ à partir de la seule connaissance de $k$, sans connaître les nombres précédents. Elle demande pour cela à une deuxième personne de l'assistance, qui dispose d'une calculatrice, d'effectuer les opérations suivantes :
- multiplier $k$ par la racine carrée de 5,
- ajouter $k$ à ce produit,
- ajouter encore $1$,
- diviser le tout par $2$,
- prendre enfin la partie entière.
Si il n'y a pas eu d'erreur de calcul, le nombre obtenu coïncide avec le dernier nombre $\ell$ écrit sur la fiche.
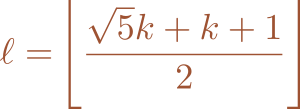
Comment ça marche ?
Les nombres calculés successivement dans les cellules peuvent tous s'exprimer en fonction des deux premiers nombres $a$ et $b$ choisis par la personne volontaire : $$ c = a + b, $$ $$ d = a + 2b, $$ $$ e = 2a + 3b, $$ $$ f = 3a + 5b, $$ $$ g = 5a + 8b, $$ $$ \cdots $$ $$ k = 34a + 55b, $$ $$ \ell = 55a + 89b. $$ On s'aperçoit (et on le vérifie facilement) que les coefficients successifs de $a$ dans ces expressions sont les nombres de la suite de Fibonacci, de même que les coefficients de $b$ (mais avec un décalage de un rang). Or ces nombres vérifient une propriété bien connue : le quotient entre deux nombres de Fibonacci successifs se rapproche très vite du nombre d'or. On en déduit qu'il en est de même pour la suite de nombres calculés sur la fiche, en particulier le quotient $\ell/k$ doit être très proche du nombre d'or : $$ \dfrac{\ell}{k}\simeq\varphi=\dfrac{1+\sqrt{5}}{2}. $$ L'idée est donc de calculer le produit de $k$ par le nombre d'or, puis de prendre le nombre entier le plus proche. C'est précisément le calcul effectué par la suite des opérations décrite ci-dessus. Le quotient de deux nombres de Fibonacci successifs se rapproche suffisamment vite du nombre d'or pour que, quels que soient les nombres entiers $a$ et $b$ choisis entre 1 et 20, la formule appliquée donne le bon résultat. Si on autorisait les nombres $a$ et $b$ à prendre des valeurs plus grandes, il faudrait rallonger la suite des nombres calculés sur la fiche pour être sûr de retrouver le dernier nombre à partir de l'avant-dernier.
Aller à la page regroupant toutes les activités sur Fibonacci.