- Solution 1 (proposée par Olivier Monnom, Mt-St-Guibert)
- Solution 2 (proposée par Pierre Renfer, Ostwald)
- Pour ceux que ça intéresse : un peu de théorie des groupes autour du jeu Recto-Verso.
Solution 1, proposée par Olivier Monnom, Mt-St-Guibert (Belgique)
Soit la grille 3x3 sur laquelle les 9 positions sont partitionnées en 4 ensembles disjoints A,B,C et D.
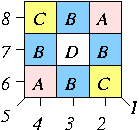
Numérotons les 8 mouvements possibles de 1 à 8 (les mouvements 1 et 5 sont les mouvements diagonaux).
Dans une configuration donnée, un ensemble est dit pair (respectivement impair) si le nombre de pions noirs dans cet ensemble est pair (respectivement impair). Observons que
- (1) Le mouvement 1 ne change pas la parité de l'ensemble C.
- (2) Le mouvement 5 ne change pas la parité de l'ensemble A.
- (3) Les mouvements 3 et 7 ne changent pas la parité de l'ensemble B.
- (4) Un mouvement quelconque 2 OU 4 OU 6 OU 8 change simultanément la parité des 3 ensembles A ET B ET C.
- (5) La suite des mouvements 1 3 5 6 8 change l'état de D sans affecter les autres ensembles.
Prouvons qu'un état est accessible si et seulement si les 3 ensembles A, B et C sont simultanément pairs ou simultanément impairs (peu importe l'état de D, d'après (5)).
Condition nécessaire
- les actions décrites en (1), (2) et (3) gardent la parité des ensembles A, B et C.
- Les actions décrites en (4) changent simultanément la parité de tous les ensembles A, B et C.
Donc, compte tenu des conditions initiales (A, B, C pairs), toute configuration atteinte le sera avec soit des ensembles A, B et C tous pairs, soit avec des ensembles A, B et C tous impairs.
Condition suffisante
Cas 1. Supposons les ensembles A, B et C tous pairs, et les pions de B diamétralement opposés de même couleur. Alors il est facile par une (des) action(s) (1) et/ou (2) et/ou (3) de rendre blancs tous les pions de A union B union C.
Cas 2. Supposons les ensembles A, B et C tous pairs, et les pions de B diamétralement opposés de couleurs différentes. Alors en effectuant les mouvements 6 puis 4 on se ramène au cas 1.
Cas 3. Supposons les ensembles A, B et C tous impairs, alors par une action A4, on se ramène au cas 1 ou au cas 2.
Calculons le nombre de configurations possibles.
| État | A | B | C | D | Total |
| pair | 2 | 8 | 2 | 2 | 64 |
| impair | 2 | 8 | 2 | 2 | 64 |
Soit 128 combinaisons possibles parmi 29=512. Si quelqu'un place les pions au hasard il a donc 128/512= 1 chance sur 4 d'obtenir une configuration accessible.
Solution 2, proposée par Pierre Renfer, Ostwald (France)
Majoration du nombre de configurations accessibles
Notons L1, L2, L3 les lignes du haut vers le bas, C1, C2, C3 les colonnes de la gauche vers la droite, D1 la diagonale principale (passant par la case supérieure gauche) et D2 l'autre diagonale. On notera avec le même symbole la transformation retournant les pions de la rangée correspondante.
Soit G le groupe engendré par ces tranformations. Comme les générateurs commutent entre eux, le groupe G est abélien.
On remarque que L1 ο L2 ο L3 = C1 ο C2 ο C3, et on peut donc supprimer par exemple L2 de la liste des générateurs.
On peut par ailleurs y remplacer C2 par la transformation A := C2 ο L1 ο L3 ο D1 o D2, qui est très simple puisqu'elle retourne uniquement le pion central.
On peut encore simplifier en remplaçant respectivement D1 et D2 par E1 := A ο D1 et E2 := A ο D2.
Tout élément T de G s'écrit donc
T = Aa ο L1l1 ο L3l3 ο C1c1 ο C3c3 ο E1e1 ο E2e2,
où les exposants valent 0 ou 1.
On ne sait pas encore que les exposants sont définis de façon unique, mais il est déjà sûr que l'ordre de G est au maximum 27. Le nombe de configurations étant 29, un quart d'entre elles au maximum seront accessibles.
Détermination des configurations accessibles
Montrons maintenant que les exposants de l'écriture de T ci-dessus sont uniques. Observons la configuration image par T de la configuration initiale.
Comme L1 est le seul générateur retournant le pion du milieu de la première ligne, l'exposant l1 est déterminé : Il vaut 0 ou 1 suivant la couleur du pion sur cette case. De façons analogues les exposants l3, c1 et c3 sont déterminés.
Comme A est le seul générateur renversant le pion de la case centrale du carré, l'exposant a est aussi déterminé.
Soit alors
S:= Aa ο L1l1 ο L3l3 ο C1c1 ο C3c3 ο T = E1e1 ο E2e2,
Observons la configuration image par S de la configuration initiale : Elle a des pions blancs au centre du carré et aux centres des rangées L1, L3, C1, C3.
Il reste exactement quatre possiblilités pour cette configuration :
 |
 |
 |
 |
| e1 = e2 = 0 | e1 = e2 = 1 | e1 = 1 et e2 = 0 | e1 = 0 et e2 = 1 |
Finalement l'ordre du groupe G est bien 27. La probabilité de former une configuration accessible est donc 1/4.
De plus, la démonstration précédente donne un moyen de voir si une configuration est accessible ou non : on détermine les valeurs de a, l1, l3, c1 et c3, et l'on regarde si l'on obtient ou non l'une des quatre configurations ci-dessus.
Lien avec un résultat de théorie des groupes
Comme le montre en particulier la solution 1 ci-dessus, le problème Recto-Verso peut être résolu sans faire appel à aucune connaissance mathématique particulière. Cependant, il permet d'illustrer de façon amusante un résultat de théorie des groupes.
Ainsi que l'a remarqué l'auteur de la solution 2, l'ensemble G des transformations permises par la règle du jeu forme un groupe commutatif. En fait, on peut voir G comme un sous-groupe d'un groupe Γ un peu plus gros : le groupe Γ engendré par les 9 retournements P1,...,P9 des pions pris individuellement. Chacun des générateurs élémentaires de G est la composée de 3 retournements individuels : par exemple, L1 = P1 ο P2 ο P3.
Formulons quelques observations élémentaires sur le groupe Γ.
- Γ est toujours un groupe commutatif.
- On peut identifier chaque transformation dans Γ à la partie des pions retournés par cette transformation. Il y a donc autant d'éléments dans Γ que de parties de l'ensemble des 9 cases, soit 29.
- Toute transformation dans Γ est d'ordre (au plus) 2. Autrement dit, répéter deux fois de suite une transformation dans Γ revient à ne rien faire du tout !
Dual d'un groupe commutatif fini
Γ étant un groupe commutatif fini, on appelle dual de Γ l'ensemble des morphismes de groupe de Γ dans le groupe multiplicatif des nombres complexes non nuls. Muni de la multiplication, le dual de Γ est lui aussi un groupe commutatif fini, qui est toujours isomorphe à Γ.
Dans le cas du groupe Γ qui nous intéresse, tout élément γ vérifie γ ο γ = Id, et donc pour tout χ dans le dual, on a
χ(γ)2 = χ(γ ο γ) = χ(Id) = 1.
Tout χ dans le dual est donc à valeurs dans {-1,1}. Observons les valeurs prises par χ sur les générateurs P1,...,P9 de Γ : il y a les indices j tels que χ (Pj) = -1, et ceux tels que χ (Pj) = 1. Notons A la partie de l'ensemble des 9 cases correspondant aux indices j tels que χ (Pj) = -1. Pour γ dans Γ, χ (γ) vaut alors 1 si le nombre de pions de A retournés par γ est pair, -1 si ce nombre est impair.
Caractérisation d'un sous-groupe par dualité
Pour G sous-groupe de Γ, on appelle orthogonal de G l'ensemble des χ dans le dual de Γ qui prennent la valeur 1 en tout élément de G. L'orthogonal de G est un sous-groupe du dual, isomorphe au quotient Γ/G. Par définition, il est évident que tout g dans G vérifie
quel que soit χ dans l'orthogonal de G, χ (g) = 1.
Or, un joli théorème dit que cette propriété n'est vérifiée que par les éléments du sous-groupe G. Autrement dit, elle permet de caractériser le sous-groupe G.
Venons-en au cas du sous-groupe G engendré par les retournements rangée par rangée. Ce groupe étant de cardinal 27, le quotient de Γ par G est de cardinal 4, et donc l'orthogonal de G possède 4 éléments. Il existe donc 4 parties de l'ensemble des 9 cases telles que pour tout g ∈ G, le nombre de pions retournés par g dans chacune de ces 4 parties est pair, et ceci caractérise les transformations dans G !
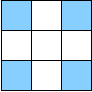
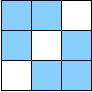
L'une des 4 parties est à la fois évidente et inintéressante : c'est l'ensemble vide (qui correspond à l'élément neutre dans le dual). En cherchant un petit peu, on trouve assez facilement les 3 autres parties de l'orthogonal de G, qui sont représentées ici en bleu.
 |
 |
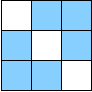 |
| A1 | A2 | A3 |
On peut remarquer que si le nombre de pions retournés par une transformation γ est pair dans deux des trois parties A1,A2,A3, alors il est pair dans la troisième. Ainsi, la parité du nombre de pions noirs dans (au moins) deux des parties ci-dessus caractérise les configurations accessibles. Cette propriété est bien sûr équivalente à chacune des caractérisations données dans les solutions 1 et 2 !

