La démonstration qui suit, due à J.Lubczanski, est à la portée de monsieur "Tout le monde" !
Voici, dans l'ordre, les 3 idées qui charpentent la démonstration du théorème de Pick :
- On va découper le polygone en triangles élémentaires, c'est à dire en triangles n'ayant aucun point du quadrillage comme point "intérieur" ou comme point sur le bord (autre que ses sommets).
- On va vérifier la formule de Pick pour un triangle élémentaire.
- On va montrer que si la formule de Pick est vraie pour un polygone P et pour un triangle élémentaire T, elle est encore vraie pour le polygone issu de l'assemblage de P et T.
À présent voici, pour chacune de ces idées, une preuve...
Première idée
Le découpage se déroule en quatre phases successives :
Première phase : On découpe le polygone en polygones convexes.
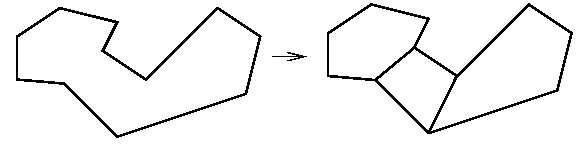
Deuxième phase : On découpe chaque polygone convexe en triangles, en traçant toutes les diagonales partant d'un même sommet.
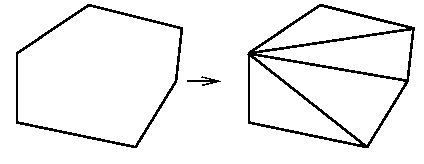
Troisième phase : On découpe chaque triangle en triangles n'admettant aucun point du quadrillage comme point "intérieur". Pour cela, on relie un point "intérieur" aux trois sommets de ce triangle. On obtient trois nouveaux triangles dans chacun desquels on réitère ce procédé. Au bout du compte, on aura partitionné le triangle initial en triangles sans point "intérieur".
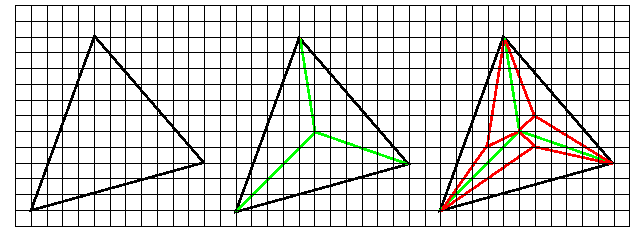
Quatrième phase : On découpe chaque triangle sans point intérieur en reliant les points sur les bords d'un côté au sommet opposé. On réitérant le procédé jusqu'à l'obtention de triangles élémentaires.
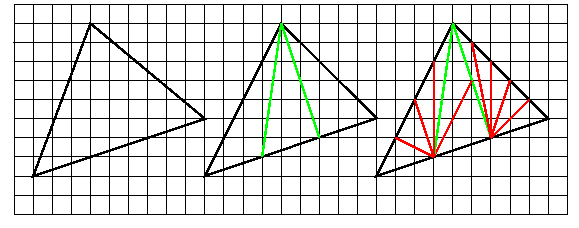
Deuxième idée
Tout triangle élémentaire a trois points sur le bord (ses sommets) et aucun point "intérieur". D'après la formule de Pick, son aire vaut 1/2. Nous devons donc vérifier que tout triangle élémentaire a une aire qui vaut 1/2. Pour cela, on va calculer l'aire du parallélogramme obtenu en réunissant ce triangle et son symétrique par rapport au milieu d'un de ses côtés.
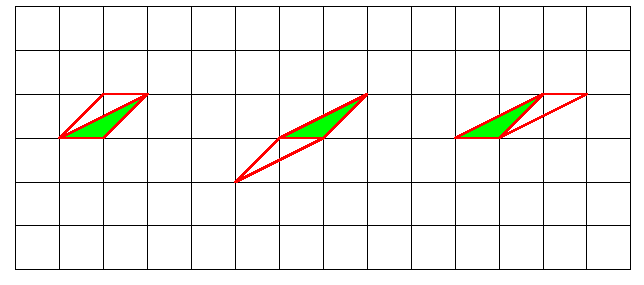
Grâce aux propriétés de la symétrie centrale, on voit que le quatrième point obtenu pour construire
le parallélogramme sera nécessairement un point du quadrillage.
À partir de ce parallélogramme, on construit un nouveau quadrillage en considérant toutes les
parallèles aux côtés du parallélogramme passant par les noeuds du quadrillage originel.
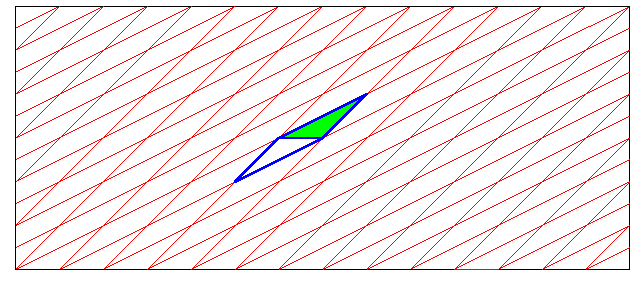
Ce second quadrillage est défini de manière unique.
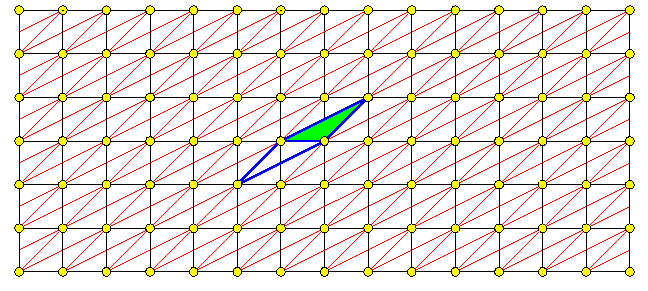
Clairement, chaque noeud du premier quadrillage est encore un noeud du second, et puisque le parallélogramme
n'a pas de point "intérieur" et de point sur les bords (autres que ses sommets), chaque noeud du second est
un noeud du premier.
Ainsi, chaque quadrillage détermine le même réseau de points, on dit que ces deux quadrillages sont équivalents.
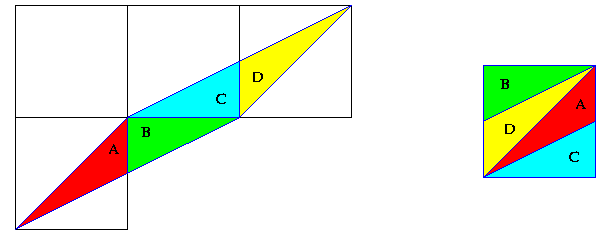
On va maintenant montrer que les figures de base de deux quadrillages équivalents ont même surface :
En effet, si un parallélogramme est découpé par des carrés en plusieurs parties A, B, C, D,... chaque point
d'un carré est dans une région soit de type A, soit de type B,...
Ceci garantit que le carré est exactement recouvert par la réunion d'une région de type A, d'une région de type B,...
Le parallélogramme a donc la même aire que le carré.
On en déduit alors que l'aire d'un triangle élémentaire vaut 1/2.
Troisième idée
On suppose que la formule de Pick est vraie pour un polygone P et pour un triangle élémentaire T.
Si I et B sont respectivement le nombre de points "intérieurs" et sur le bord de P, l'aire du polygone assemblé P U T vaut I+B/2-1+1/2 puisque l'aire de T vaut 1/2.
On a deux facons d'assembler un polygone avec un triangle élémentaire :
Soit par un côté commun, dans ce cas le polygone assemblé P U T aura autant de points "intérieurs" que P
et un point sur le bord en plus. La formule de Pick s'écrit I+(B+1)/2-1.
Soit par deux côtés communs, dans ce cas P U T aura un point "intérieur" de plus que P et un point sur le
bord en moins. La formule de Pick s'écrit I+1+(B-1)/2-1.
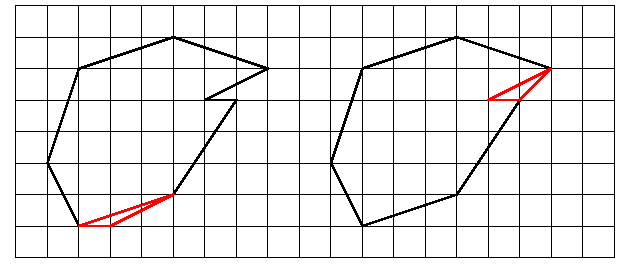
Dans les deux cas, on retrouve bien l'aire de P U T.
Conclusion
Par récurrence, la formule de Pick est vraie pour tout polygone.

