De nombreuses grandeurs statistiques résultent de la combinaison d'un grand nombre de paramètres sans rapport les uns avec les autres. Par exemple, la taille d'un individu dépend de multiples facteurs génétiques, mais aussi de son régime alimentaire, de ses éventuels problèmes de santé, des soins dont il a bénéficié, etc. Quand on représente la répartition statistique d'une telle grandeur sous forme d'un histogramme, on constate souvent que celui-ci forme une sorte de cloche centrée autour d'une valeur moyenne.
La planche de Galton, du nom de son inventeur Sir Francis Galton (1822-1911), est un dispositif destiné à visualiser la loi des écarts à la moyenne dans le cadre d'une série d'un grand nombre d'expériences aléatoires indépendantes.
Des billes roulent à la surface d'une planche inclinée sur laquelle sont disposés des clous en quinconce (d'où le nom anglais «quincunx»). Les billes passent aléatoirement d'un côté ou de l'autre des clous, et on mesure à l'arrivée la quantité de billes en fonction de leur position à la sortie de la planche. Cette position résulte de l'addition de toutes les déviations qu'elles ont subies en tombant sur ces clous : chacune de ces déviations est une expérience aléatoire indépendantes des autres. Puisque les déviations vers la droite sont aussi probables que celles vers la gauche, la trajectoire « moyenne » est verticale.
La distribution des billes dans les colonnes d'arrivée est régie par deux résultats fondamentaux de la théorie des probabilités : la loi des grands nombres et le théorème central limite, qui sont ainsi concrètement mis en évidence.
La probabilité d'arrivée de la bille et le théorème central limite
Une bille étant lâchée en haut de la planche, la distribution des probabilités suivant laquelle elle arrivera dans telle ou telle colonne est un classique en théorie des probabilités discrètes : c'est ce que l'on appelle la loi binomiale. Toutes les trajectoires possibles étant équiprobables, la probabilité que la bille finisse sa course dans une colonne donnée est proportionnelle au nombre de chemins qui mènent du haut de la planche à la colonne visée. Ce nombre de chemins est un coefficient binomial, donné par le triangle de Pascal.
Sur la figure ci-dessous, on a représenté graphiquement pour chaque colonne la probabilité qu'une bille partant du haut de la planche finisse sa course dans cette colonne (ici, il y a 60 rangées de clous). Notez que toutes les colonnes sont théoriquement accessibles, mais si l'on s'écarte un peu du milieu, la probabilité devient si faible qu'elle n'est plus visible à l'échelle utilisée ! La raison est simple : il y a beaucoup plus de chemins menant aux colonnes centrales qu'à celles qui s'écartent du centre. Ainsi, il n'existe qu'un seul chemin menant à chacune des colonnes extrèmes, alors qu'il y a des milliards de façons d'arriver à la colonne centrale.
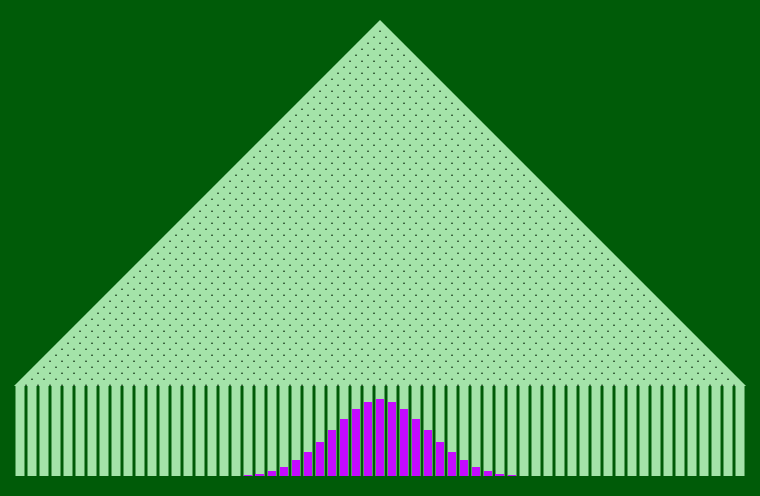
On constate sur ce graphique que la distribution de probabilité d'arrivée dans les colonnes semble dessiner une courbe en cloche très régulière. Le théorème central limite dit précisément que plus le nombre de rangées de clous sur la planche est grand, plus la distribution des probabilités d'arrivées se rapproche de cette courbe en cloche, appelée courbe de Gauss. (En fait, ce cas précis est un cas particulier d'application du théorème central limite, qui porte le nom de théorème de Moivre-Laplace.) La largeur de la cloche varie en fonction de la taille de la planche : elle est de l'ordre de la racine carrée du nombre de rangées. Ainsi, multiplier le nombre de rangées par 4 ne fait que doubler la largeur de la cloche. La distribution de probabilité qui correspond à cette courbe limite s'appelle la loi normale.
La répartition observée des billes et la loi des grands nombres
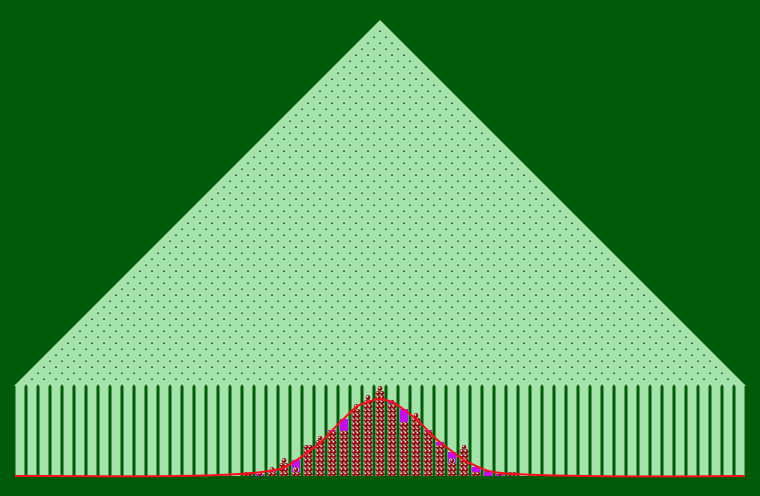
En haut de la planche, chaque bille a donc une probabilité d'arrivée qui suit la forme de cloche représentée ci-dessus. Mais après sa descente elle ne touche évidemment qu'une seule des colonnes ! Pour visualiser en pratique la distribution d'arrivée, on doit répéter un grand nombre de fois l'expérience, c'est-à-dire lancer un grand nombre de billes. Chacune suit une trajectoire indépendante des autres, et c'est ici que la loi des grands nombres intervient : plus le nombre de billes utilisées est grand, plus la proportion des billes arrivées dans chaque colonne se rapproche de la probabilité théorique.
Sur la figure ci-dessous, où un peu plus de 300 billes ont été lancées, on observe une répartition empirique suivant grossièrement la courbe en cloche. En utilisant beaucoup plus de billes, le résultat se rapprocherait plus encore de la distribution théorique.
