Triangle de Dudeney

Solution 1, proposée par Lucien Verney, Rouen
Une question supplémentaire, posée par Lucien Verney
Solution 2, proposée par Pierre Renfer, Ostwald
L'amoureux indécis, une question supplémentaire posée par Pierre Renfer

Solution 1, proposée par Lucien Verney, Rouen

Notons |MNP| l'aire d'un triangle quelconque MNP. Puisque CA'=CB/3, l'aire |AA'C| vaut |ABC|/3. De même pour |BB'A| et |CC'B|, et donc

|AA'C|+|BB'A|+|CC'B|=|ABC|.

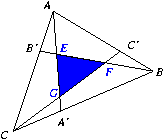
Mais dans la somme des trois aires à gauche, chacun des triangles CGA', AEB' et BFC' est compté deux fois, alors que le triangle EFG n'est pas compté du tout. On en déduit

|CGA'|+|AEB'|+|BFC'|=|EFG|,

ce qui répond à la question 1.

Pour tout point P du plan et tout réel r, notons h_P,r l'homothétie de centre P et de rapport r.On a par les hypothèses de construction de la figure :

A'=h_C,1/3(B), et B=h_C',-1/2(A).

La composé des 2 homothéties h_C,1/3oh_C',-1/2 est une homothétie dont le rapport est le produit des 2 rapports, soit -1/6, et son centre est aligné avec les centres C et C', mais aussi avec A et A' : c'est donc G. Autrement dit

A'=h_G,-1/6(A).

Le même raisonnement, en écrivant cette fois A'=h_B,2/3(C), et C=h_B',-2(A), prouve aussi que

A'=h_E,-4/3(A).

On en déduit que E est le milieu de [GA]. De même, F est le milieu de [EB] et G est le milieu de [FC].

Enfin, en utilisant encore le fait que A'=h_G,-1/6(A), on obtient

|CGA'|=|AA'C|/7,

et de même

|AEB'|=|ABB'|/7, et |BFC'|=|BCC'|/7.

Grâce au résultat de la question 1, on en conclut que

|EGF|=|ABC|/7.

Question

Par quoi doit-on remplacer 1/3 dans l'énoncé pour que l'aire du triangle EFG soit la moitié de l'aire du triangle ABC ?

Solution 2, proposée par Pierre Renfer, Ostwald

On peut obtenir les coordonnées barycentriques dans le repère (A,B,C) de tous les points de la figure.

A : (1,0,0)
B : (0,1,0)
C : (0,0,1)
A' : (0,1,2)
B' : (2,0,1)
C' : (1,2,0)

La droite (AA') a pour équation z = 2y. La droite (BB') a pour équation x = 2z. Donc le point E a pour coordonnées (4,1,2). Par permutation circulaire, on obtient

E : (4,1,2)
F : (2,4,1)
G : (1,2,4)

En divisant par 7, on obtient pour E, F et G les coordonnées de somme 1. En divisant par 3, on obtient pour A',B' et C' les coordonnées de somme 1. On vérifie facilement sur les coordonnées de somme 1, que E, F et G sont respectivement milieux de AG, BE et CF.

En choisissant l'aire du triangle ABC comme unité d'aire, on obtient l'aire d'un triangle MNP comme valeur absolue du déterminant dont les trois colonnes sont les coordonnées de somme 1 des trois points M,N et P. On touve que les triangles AEB', BFC' et CGA' ont chacun 1/21 comme aire et que le triangle EFG a pour aire 1/7.

L'auteur de la solution 2 propose aussi une jolie histoire autour de cette figure.

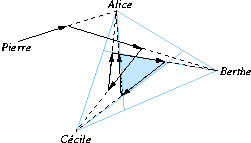
L'amoureux indécis

Il s'agit d'un garçon (Pierre), amoureux de trois charmantes jeunes filles : Alice, Berthe et Cécile, habitant respectivement en A , B et C. Pierre part d'un point P et marche en direction d'Alice, mais à mi-chemin il change d'avis et se dirige vers Berthe, puis change encore d'avis à mi-chemin et se dirige vers Cécile, puis, pris de remors à mi-chemin, se dirige à nouveau vers Alice, etc.

Si le point P est placé en G , il est condamné à décrire éternellement le triangle GEF.

Question

Montrer que, quel que soit le point P de départ, Pierre arrivera asymptotiquement sur le circuit GEF.

P.S. Toujours pas de réponse à la question subsidiaire : pourquoi cette figure porte-t-elle le nom de triangle de Dudeney ?