Choisissons un point I sur la droite (F), et traçons les points G et M
sur cette droite tels que I soit le milieu de BG et G le milieu de IM.
G sera le centre de gravité et M le pied de la médiane
issue de B, de notre triangle isocèle.
Les points A et C sont sur la droite (H) passant par M et perpendiculaire à (D).
D'autre part, la médiane issue de A est aussi médiatrice de notre triangle isocèle en A,
et donc le centre de gravité du triangle ABC est à égale distance des points B et C.
C est donc l'un des points intersection de la droite (H) et du cercle de centre G et de rayon GB.
On obtient facilement le point A comme symétrique du point C par rapport au point M.
Pour chaque choix du centre de gravité, il existe deux triangles répondant à la question posée.
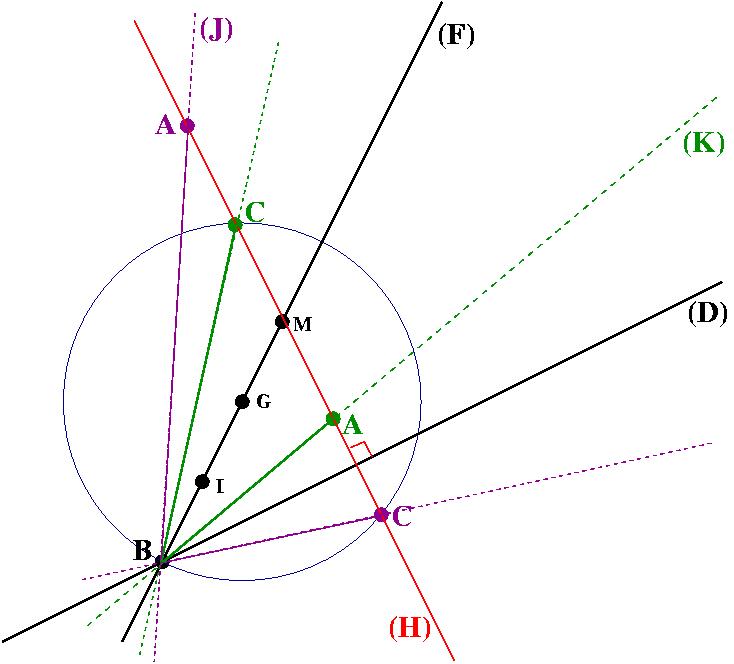
Remarques
- Si les droites (D) et (F) sont perpendiculaires, il n'y a pas d'autre solution que les points A, B et C confondus.
- Les points A appartiennent toujours à l'une des 2 droites (J) ou (K).
Pierre RENFER nous a adressé une solution légèrement différente. Il a remarqué que les points A, satisfaisant la relation AB=2AM, doivent donc appartenir au cercle de diamètre GV où G est le barycentre de (B,1) et (M,2) et V le barycentre de (B,1) et (M,-2).

