Problème
On considère une chambre, dont le parquet est formé de lames parallèles. On laisse tomber une aiguille sur le plancher. Quelle est la probabilité pour que celle-ci tombe sur l'une des rainures séparant les lames du parquet?

Ce problème est dû à Georges-Louis Leclerc (1707-1788), comte de Buffon, connu pour son œuvre naturaliste (en particulier une Histoire naturelle en 44 volumes), mais aussi mathématicien et philosophe. Il figure dans son Essai d'arithmétique morale, publié en 1733, au chapitre concernant le « mémoire sur le jeu du franc carreau » . Ce jeu consistait à l'époque à parier si une pièce de monnaie lancée sur un carrelage allait tomber en plein dans un carreau ou toucher l'un des joints séparant les carreaux. Dans son essai, présenté pour entrer à l'Académie royale des sciences de Paris, Buffon calcule la probabilité de gagner à ce jeu, puis l'étend au cas du lancer d'une aiguille. La variante de l'aiguille est plus complexe, car on doit tenir compte de l'orientation de l'aiguille lorsqu'elle tombe : la pièce de monnaie étant circulaire, son orientation n'influe pas sur ses chances de tomber sur une rainure. Le problème de l'aiguille de Buffon est resté célèbre car c'est entre autre la première expérience aléatoire qui fait apparaître le nombre $\pi$ et permet d'en donner une approximation.
Le résultat obtenu par Buffon est le suivant :
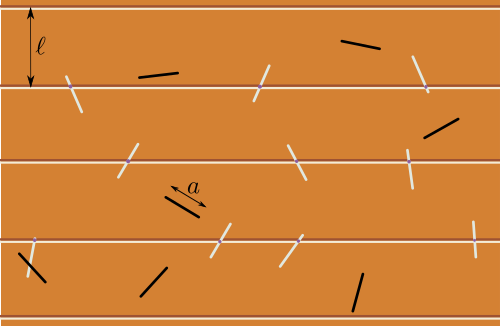
On lance une aiguille de longueur $a$ sur un parquet dont les lames ont pour largeur $\ell$. Alors la probabilité que l'aiguille tombe à cheval sur deux lames est $$p=\frac{2a}{\pi \ell}.$$
Une estimation de $\pi$
Dans l'animation, les aiguilles lancées ont pour longueur la moitié de la largeur des lames : $a=\ell/2$. On a ainsi $p=1/\pi$. Si on lance un grand nombre d'aiguilles, on peut estimer « raisonnablement » la probabilité $p$ par la proportion d'aiguilles lancées ayant touché une rainure. Ici, « raisonnablement » signifie qu'avec probabilité 1, cette proportion se rapproche de $1/\pi$ quand le nombre d'aiguilles lancées devient très grand ; c'est une conséquence de la loi des grands nombres. On dit que cet estimateur est consistant. Inversement, en divisant le nombre d'aiguilles lancées par le nombre d'aiguilles ayant touché une rainure, on obtient donc un estimateur consistant de $\pi$.
Cependant la vitesse à laquelle on se rapproche de $\pi$ est relativement lente (de l'ordre de 1 sur la racine carrée du nombre d'aiguilles lancées). Ainsi pour diviser par 10 l'erreur d'approximation obtenue, il faut lancer 100 fois plus d'aiguilles (c'est cette fois une conséquence du théorème central limite).
Remarquons que l'estimation obtenue donne un nombre rationnel : c'est la fraction de deux nombres entiers, alors que $\pi$ est irrationnel.

Expérience sur les aiguilles de Buffon menée à l'occasion de la Fête de la Science. Au stade présenté sur la photo, l'estimation de $\pi$ est étonnamment précise pour le nombre d'aiguilles lancées : $$ \frac{799}{254} \simeq 3,1456. $$
Des aiguilles aux nouilles, le « spaghetti de Buffon »
Voici l'idée générale d'une démonstration du résultat de Buffon, due à Joseph-Émile Barbier [1]. Au lieu de chercher la probabilité $p$ d'intersection de l'aiguille avec les rainures du parquet, on s'intéresse au nombre moyen $\mathcal E$ d'intersections de la courbe avec les rainures du parquet, aussi appelé espérance du nombre d'intersections.
Le lien avec la probabilité $p$ est le suivant : dans le cas d'une aiguille rectiligne de longueur $a$ plus petite que $\ell$, il y a au plus une intersection de l'aiguille avec les rainures du plancher. On a donc $\mathcal E= p$.
Imaginons que l'on marque un point au milieu de l'aiguille lancée, pour la séparer en deux demi-aiguilles de même longueur. Le nombre moyen de croisements de l'aiguille longue se calcule comme la somme du nombre moyen de croisements de la première demi-aiguille et du nombre moyen de croisements de la seconde demi-aiguille.
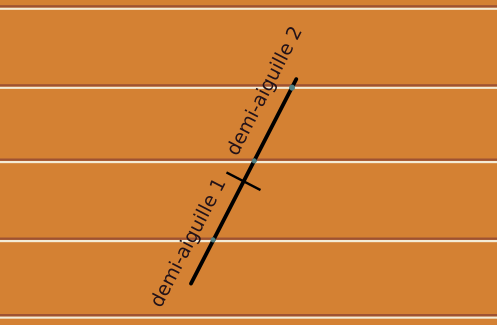
Considérons ensuite le cas d'une aiguille qui a été déformée et a pris la forme d'une ligne brisée. Le nombre moyen d'intersections de cette ligne avec les rainures du parquet s'obtient comme la somme des nombres moyens d'intersections de chacun des segments de la ligne brisée.
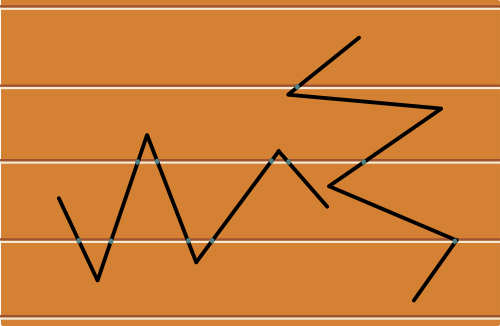
Supposons maintenant que l'aiguille ait une forme courbe, disons une nouille (rigide), dont on note toujours $a$ la longueur. Dit en anglais, on passe donc de « Buffon's needle » à « Buffon's noodle » [2] !
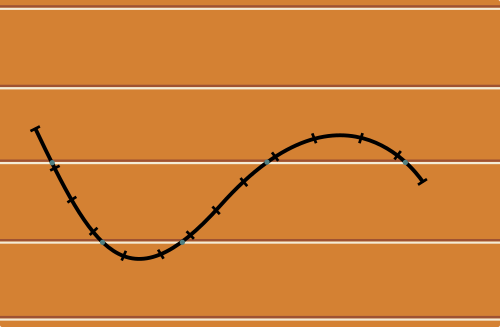
Si on coupe la courbe en tout petits morceaux de même longueur, ceux-ci peuvent être considérés comme de petits segments de droite. Alors le nombre moyen d'intersections est le même pour chaque segment. Ainsi, le nombre moyen d'intersections $\mathcal E$ est proportionnel au nombre de petits segments, donc à la longueur $a$ de la courbe : $$\mathcal E=ca.$$ Il s'agit de déterminer la constante $c$, qui est la même quelle que soit la courbe choisie.
Si cette courbe est un cercle de diamètre égal à la largeur $\ell$ des lames de parquet, alors, d'une part sa longueur est $a=\pi \ell$, et d'autre part, le nombre d'intersections avec les rainures du parquet est toujours égal à $2$ : il ne dépend pas de la manière dont tombe le cercle. Le nombre moyen d'intersections est donc $\mathcal E=2$.
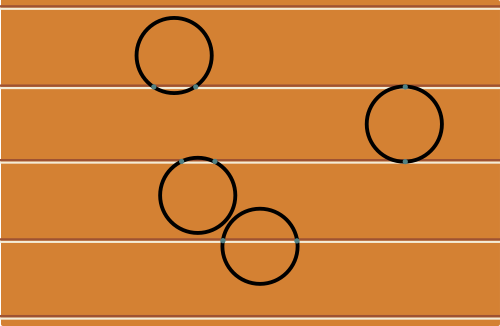
Donc, $2=c\pi \ell$, et ainsi $c=2/(\pi \ell)$. On en déduit finalement $$\mathcal E=\frac{2a}{\pi \ell}.$$
Une conséquence : le théorème de Barbier
On peut déduire du raisonnement ci-dessus un résultat surprenant. Pour une courbe fermée, on appelle largeur ou diamètre dans une certaine direction la largeur minimale d'une lame de parquet orientée dans cette direction qui peut complètement contenir la courbe. La courbe est dite de largeur constante lorsque cette largeur est la même quelle que soit l'orientation choisie pour la lame de parquet. L'exemple le plus classique de courbe de largeur constante est le cercle. Le triangle de Reuleaux ci-dessous en est un autre.
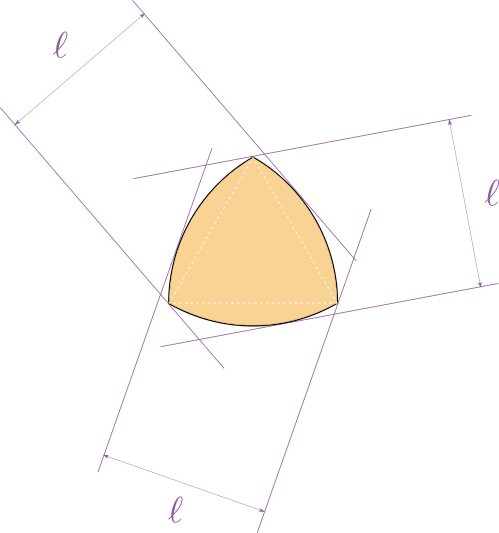
Le triangle de Reuleaux est formé de 3 arcs de cercles, chacun centré sur l'un des sommets d'un triangle équilatéral, et délimité par les deux autres sommets.
Barbier a prouvé le théorème suivant :
Le périmètre d'une courbe fermée de largeur constante ne dépend pas de sa forme : précisément, toute courbe fermée de largeur constante $\ell$ a pour périmètre $\pi \ell$.
Voici une explication. On imagine qu'on lance une courbe de largeur constante $\ell$ sur un parquet dont les lames sont également de largeur $\ell$. Cette courbe a donc exactement 2 intersections avec les rainures du parquet. Par ailleurs, le raisonnement ci-dessus assure que le nombre moyen d'intersections vaut ${\mathcal E}=2a/\pi \ell$ où $a$ est le périmètre de la courbe. On a donc $2=2a/\pi \ell$, soit $a=\pi \ell$.
Références
[1] Joseph-Émile Barbier. Notes sur le problème de l’aiguille et le jeu du joint couvert, Journal de Mathématiques Pures et Appliquées, vol. 5 (1860), p. 273–286.
[2] Ramaley, J.F. Buffon's Noodle Problem. The American Mathematical Monthly, vol. 76 (8, Octobre 1969), p. 916–918.
Aller à l'animation sur les aiguilles de Buffon.
Aller à la page regroupant les activités autour du nombre $\pi$.