En général, on ne peut pas diviser un angle en 3 parties égales à l'aide d'une règle et d'un compas (Théorème de Pierre-Laurent Wantzel, 1837). Mais la trisection de l'angle est réalisable par origami. La construction suivante est due à Hisashi Abe (1980).
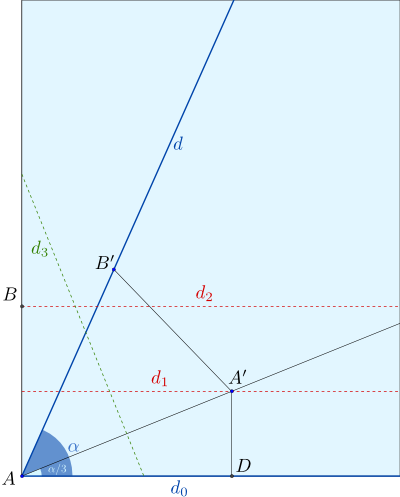
- Sur une feuille de papier, tracer la droite $d$ passant par un coin $A$ de la feuille, de telle sorte que $d$ forme, avec le bord inférieur $d_0$ de la feuille, l'angle de mesure $\alpha$ à couper en trois.
- Par pliage, construire deux bandes horizontales de même largeur (arbitraire) en bas de la feuille. On note $d_1$ et $d_2$ les droites qui les délimitent. On note aussi $B$ l'intersection du bord gauche avec la droite $d_2$ .
- Plier la feuille le long d'un pli $d_3$ de sorte que le point $A$ aille sur la droite $d_1$ en un point $A'$, en même temps que le point $B$ va sur la droite $d$ en un point $B'$.
La droite $(AA')$ est alors la trisectrice de l'angle donné: l'angle formé par $d_0$ et $(AA')$ vaut $\alpha/3$.
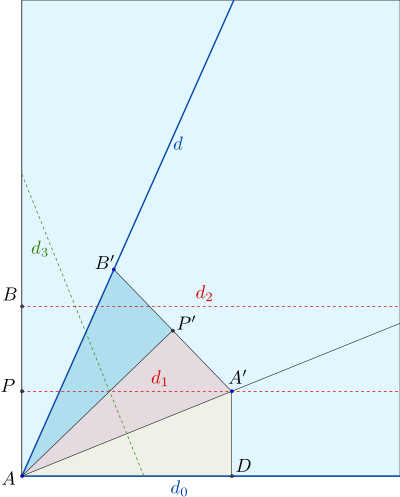
Justifions que la méthode ci-dessus fournit bien un angle de mesure $\alpha/3$.
Soient $P$ le milieu du segment $[AB]$, $P'$ celui de $[A'B']$ et $D$ le projeté orthogonal de $A$ sur $d_0$. Il suffit de montrer que les triangles $AP'B'$ , $AP'A'$ et $ADA'$ sont isométriques.
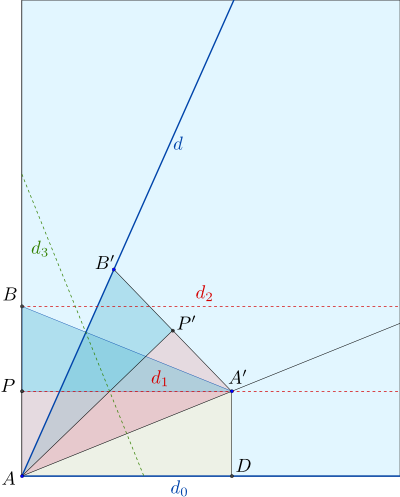
Remarquons tout d'abord que les triangles $A'PB$ et $A'PA$ sont deux triangles rectangles, symétriques par rapport à $d_1$, donc isométriques. Les triangles $AP'B'$ et $AP'A'$ sont leurs images respectives par rapport à la symétrie d'axe $d_3$, donc ce sont également deux triangles rectangles isométriques.
Enfin, notons que les triangles $ADA'$ et $A'PA$ sont également deux triangles rectangles isométriques, comme «moitiés» du rectangle $ADA'P$. Comme $A'PA$ est lui-même isométrique à $AP'A'$, on a bien montré que les trois triangles $AP'B'$, $AP'A'$ et $ADA'$ sont isométriques.